题目内容
已知:向量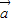 =(sinθ,1),向量
=(sinθ,1),向量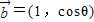 ,-
,-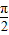 <θ<
<θ<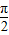 ,
,(1)若
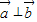 ,求:θ的值;
,求:θ的值; (2)求:
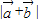 的最大值.
的最大值.
【答案】分析:(1)利用两个向量垂直的性质,两个向量垂直,数量积等于0,得到sin(θ+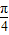 )=0,求出θ.
)=0,求出θ.
(2)由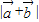 =
=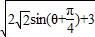 ,及-
,及-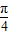 <θ+
<θ+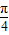 <
<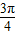 ,可得当sin(θ+
,可得当sin(θ+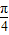 )=1时,
)=1时,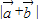 有最大值.
有最大值.
解答:解:(1)∵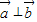 ,∴
,∴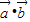 =0,
=0,
∴sinθ+cosθ=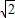 sin(θ+
sin(θ+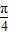 )=0.
)=0.
∵-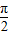 <θ
<θ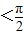 ,
,
∴θ=-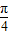 .
.
(2)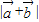 =|(sinθ+1,cosθ+1)|=
=|(sinθ+1,cosθ+1)|=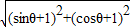 =
=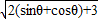
=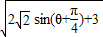 .
.
∵-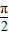 <θ
<θ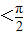 ,∴-
,∴-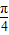 <θ+
<θ+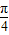 <
<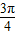 ,
,
∴当sin(θ+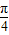 )=1时,
)=1时,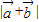 有最大值,
有最大值,
此时,θ=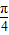 ,
,
∴最大值为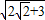 =
=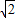 +1.
+1.
点评:本题考查两个向量的数量积的定义,数量积公式的应用,两个向量垂直的性质,求向量的模的方法.
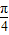 )=0,求出θ.
)=0,求出θ.(2)由
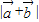 =
=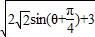 ,及-
,及-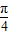 <θ+
<θ+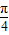 <
<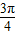 ,可得当sin(θ+
,可得当sin(θ+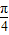 )=1时,
)=1时,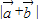 有最大值.
有最大值.解答:解:(1)∵
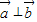 ,∴
,∴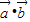 =0,
=0,∴sinθ+cosθ=
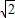 sin(θ+
sin(θ+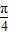 )=0.
)=0.∵-
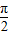 <θ
<θ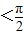 ,
,∴θ=-
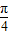 .
. (2)
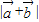 =|(sinθ+1,cosθ+1)|=
=|(sinθ+1,cosθ+1)|=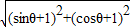 =
=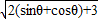
=
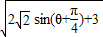 .
. ∵-
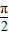 <θ
<θ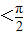 ,∴-
,∴-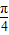 <θ+
<θ+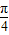 <
<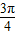 ,
,∴当sin(θ+
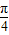 )=1时,
)=1时,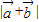 有最大值,
有最大值,此时,θ=
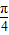 ,
,∴最大值为
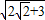 =
=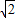 +1.
+1.点评:本题考查两个向量的数量积的定义,数量积公式的应用,两个向量垂直的性质,求向量的模的方法.

练习册系列答案
相关题目
已知:向量
=(sin
,1-cosθ),
=(cos
,
),(O为坐标原点).
(1)求
•
的最大值及此时θ的值组成的集合;
(2)若A点在直线y=2x+m上运动,求实数m的取值范围.
| OA |
| θ |
| 2 |
| OB |
| θ |
| 2 |
| 1 |
| 2 |
(1)求
| OA |
| OB |
(2)若A点在直线y=2x+m上运动,求实数m的取值范围.
已知平面向量
=(sinθ,1),
=(-
,cosθ),若
⊥
,则θ可以为( )
| a |
| b |
| 3 |
| a |
| b |
A、θ=
| ||
B、θ=
| ||
C、θ=
| ||
D、θ=
|
 =(sinθ,1),
=(sinθ,1), =(-
=(- ,cosθ),若
,cosθ),若 B.θ=
B.θ=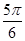 C.θ=
C.θ= D.θ=
D.θ=