题目内容
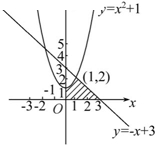
由曲线y=x2+1，直线y=-x+3及坐标轴所围成图形的面积为（ ）
分析：先确定积分区间与被积函数，再求原函数，即可求得结论．
解答：解：如图，
由方程组
，解得
或
．
∴在第一象限内，曲线y=x2+1与直线y=-x+3交于（1，2）．
∴所求围成的图形的面积
S=
（x2+1）dx+
（-x+3）dx=（
+x）
+（3x-
x2）
=
+1+3=
．
故选：C．
由方程组
|
|
|
∴在第一象限内，曲线y=x2+1与直线y=-x+3交于（1，2）．
∴所求围成的图形的面积
S=
| ∫ | 1 0 |
| ∫ | 3 1 |
| 1 |
| 3 |
| x3 |
| | | 1 0 |
| 1 |
| 2 |
| | | 3 1 |
| 1 |
| 3 |
| 10 |
| 3 |
故选：C．
点评：本题考查利用定积分求面积，先确定积分区间与被积函数，再求原函数是此类题目的共同思路和步骤．
练习册系列答案
相关题目
如图，由曲线y=x2-1，直线x=0，x=2和x轴围成的封闭图形的面积为（ ）
如图，由曲线y=x2-1，直线x=0，x=2和x轴围成的封闭图形的面积是（ ）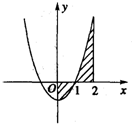
由曲线y=x2-1，直线x=0，x=2和x轴围成的封闭图形的面积（如图）可表示为（ ）