题目内容
已知A(2,-5,1),B(2,-2,4),C(1,-4,1),则向量
与
的夹角为( )
| AB |
| AC |
分析:由题意可得:
=(0,3,3),
= (-1,1,0),进而得到
•
与|
|,|
|,再由cos<
,
>=
可得答案.
| AB |
| AC |
| AB |
| AC |
| AB |
| AC |
| AB |
| AC |
| ||||
|
|
解答:解:因为A(2,-5,1),B(2,-2,4),C(1,-4,1),
所以
=(0,3,3),
= (-1,1,0),
所以
•
═0×(-1)+3×1+3×0=3,并且|
|=3
,|
|=
,
所以cos<
,
>=
=
=
,
∴
与
的夹角为60°
故选C.
所以
| AB |
| AC |
所以
| AB |
| AC |
| AB |
| 2 |
| AC |
| 2 |
所以cos<
| AB |
| AC |
| ||||
|
|
| 3 | ||||
3
|
| 1 |
| 2 |
∴
| AB |
| AC |
故选C.
点评:解决此类问题的关键是熟练掌握由空间中点的坐标写出向量的坐标与向量求模,以及由向量的数量积求向量的夹角,属于基础试题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
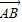 与
与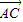 的夹角为( )
的夹角为( )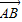 与
与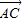 的夹角为( )
的夹角为( )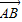 与
与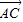 的夹角为( )
的夹角为( )