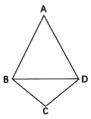
题目内容
【题目】如图,正方形ABCD和四边形ACEF所在的平面互相垂直,CE⊥AC,EF∥AC,AB=![]() ,
,![]() .
.

(1)求证:CF⊥平面BDE;
(2)求二面角A-BE-D的大小。
【答案】(1)见证明;(2) ![]() (或
(或![]() )
)
【解析】
(1)连接FG,可证得四边形CEFG为菱形,故得![]() .再根据平面ABCD
.再根据平面ABCD![]() 平面ACEF得到
平面ACEF得到![]() 平面ACEF,从而
平面ACEF,从而![]() .由线面垂直的判定定理可得结论成立.(2)建立空间直角坐标系,求出平面BDE和平面ABE的法向量,求出两向量的夹角的余弦值并结合图形可得所求角的大小.
.由线面垂直的判定定理可得结论成立.(2)建立空间直角坐标系,求出平面BDE和平面ABE的法向量,求出两向量的夹角的余弦值并结合图形可得所求角的大小.
(1)连接FG,
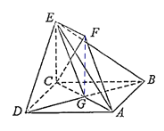
∵![]() ,
,
∴四边形CEFG为菱形,
∴![]() .
.
∵ABCD为正方形,
∴![]() ,
,
又平面ABCD![]() 平面ACEF,平面ABCD
平面ACEF,平面ABCD![]() 平面ACEF=AC,BD
平面ACEF=AC,BD![]() 平面ABCD
平面ABCD
∴![]() 平面ACEF,
平面ACEF,
∵CF![]() 平面ACEF,
平面ACEF,
∴![]() .
.
又![]() ,BD
,BD![]() 平面BDE, BG
平面BDE, BG![]() 平面BDE,
平面BDE,
∴![]() 平面BDE.
平面BDE.
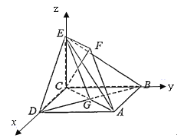
(1)∵正方形ABCD和四边形ACEF所在的平面互相垂直,且CE⊥AC,
∴CE⊥平面ABCD,
以C为原点,CB为![]() 轴,CD为
轴,CD为![]() 轴,CE为
轴,CE为![]() 轴,建立如图所示的空间直角坐标系
轴,建立如图所示的空间直角坐标系![]() ,
,
则![]() ,
,
∴![]() ,
,![]() ,
,
由(1)可得![]() 是平面BDE的一个法向量.
是平面BDE的一个法向量.
设平面ABE的一个法向量为![]()
由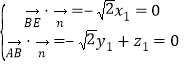 ,得
,得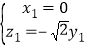 ,
,
令![]() ,得
,得![]() ,
,
∴![]() ,
,
由图形可得二面角A-BE-D为锐角,
∴二面角A-BE-D的大小为![]() (或
(或![]() ).
).

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目