题目内容
数列{an}满足an=-2n+11，则使得前n项和Sn＞0的最大值为（ ）A．8
B．9
C．10
D．11
【答案】分析：由数列的通项公式得到数列是等差数列，求出首项和公差，写出前n项和后由前n项和大于0求n得最大值．
解答：解：由an=-2n+11，所以an+1-an=-2（n+1）+11-（-2n+11）=-2，
所以数列{an}是以a1=-2×1+11=9为首项，以-2为公差的等差数列，
则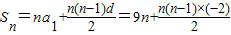
=-n2+10n，
由-n2+10n＞0，得：1＜n＜10，因为n∈N*，所以n的最大值为9．
所以使得前n项和Sn＞0的最大值为9．
故选B．
点评：本题考查了数列的函数特性，考查了等差数列的前n项和，考查了一元二次不等式的解法，此题是基础题．
解答：解：由an=-2n+11，所以an+1-an=-2（n+1）+11-（-2n+11）=-2，
所以数列{an}是以a1=-2×1+11=9为首项，以-2为公差的等差数列，
则
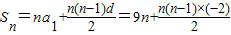=-n2+10n，由-n2+10n＞0，得：1＜n＜10，因为n∈N*，所以n的最大值为9．
所以使得前n项和Sn＞0的最大值为9．
故选B．
点评：本题考查了数列的函数特性，考查了等差数列的前n项和，考查了一元二次不等式的解法，此题是基础题．
练习册系列答案
阅读快车系列答案
相关题目