题目内容
已知数列{an},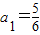 ,若以a1,a2,…,an为系数的二次方程
,若以a1,a2,…,an为系数的二次方程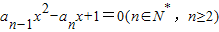 都有根α,β,且满足3α-αβ+3β=1.
都有根α,β,且满足3α-αβ+3β=1.(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=nan,求数列{bn}的前n项和Sn.
【答案】分析:(Ⅰ)将α+β=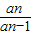 ,αβ=
,αβ=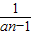 代入3α-αβ+3β=1,得an=
代入3α-αβ+3β=1,得an= an-1+
an-1+ ,故
,故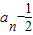 =
=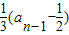 ,由此能求出数列{an}的通项公式.
,由此能求出数列{an}的通项公式.
(Ⅱ)由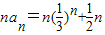 ,知
,知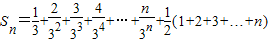 ,令Tn=
,令Tn=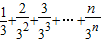 .利用错位相减法能求出数列{bn}的前n项和Sn.
.利用错位相减法能求出数列{bn}的前n项和Sn.
解答:解:(Ⅰ)∵将α+β=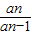 ,αβ=
,αβ=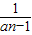 代入3α-αβ+3β=1,
代入3α-αβ+3β=1,
得an= an-1+
an-1+ ,(2分)
,(2分)
∴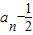 =
=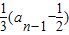 ,
,
∴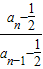 =
= 为定值.又a1-
为定值.又a1- =
= ,
,
∴数列{an- }是首项为
}是首项为 ,公比为
,公比为 的等比数列.(5分)
的等比数列.(5分)
∴an- =
= ×(
×( )n-1=(
)n-1=( )n,
)n,
∴an=( )n+
)n+ .(6分)
.(6分)
(Ⅱ)∵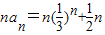 ,
,
∴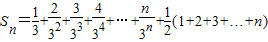 ,(7分)
,(7分)
令Tn=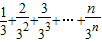 .①
.①
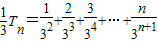 ②
②
①-②得,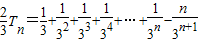 ,
,
∴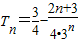 ,(11分)
,(11分)
∴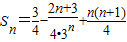 .(12分)
.(12分)
点评:本题考查数列的通项公式的求法,考查数列的前n项和公式的求法,解题时要认真审题,仔细解答,注意错位相减法的合理运用.
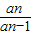 ,αβ=
,αβ=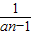 代入3α-αβ+3β=1,得an=
代入3α-αβ+3β=1,得an= an-1+
an-1+ ,故
,故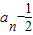 =
=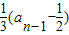 ,由此能求出数列{an}的通项公式.
,由此能求出数列{an}的通项公式.(Ⅱ)由
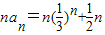 ,知
,知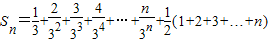 ,令Tn=
,令Tn=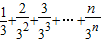 .利用错位相减法能求出数列{bn}的前n项和Sn.
.利用错位相减法能求出数列{bn}的前n项和Sn.解答:解:(Ⅰ)∵将α+β=
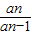 ,αβ=
,αβ=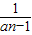 代入3α-αβ+3β=1,
代入3α-αβ+3β=1,得an=
 an-1+
an-1+ ,(2分)
,(2分)∴
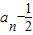 =
=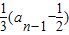 ,
,∴
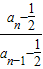 =
= 为定值.又a1-
为定值.又a1- =
= ,
,∴数列{an-
 }是首项为
}是首项为 ,公比为
,公比为 的等比数列.(5分)
的等比数列.(5分)∴an-
 =
= ×(
×( )n-1=(
)n-1=( )n,
)n,∴an=(
 )n+
)n+ .(6分)
.(6分)(Ⅱ)∵
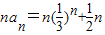 ,
,∴
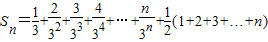 ,(7分)
,(7分)令Tn=
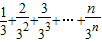 .①
.①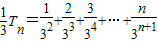 ②
②①-②得,
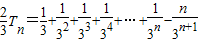 ,
,∴
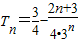 ,(11分)
,(11分)∴
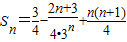 .(12分)
.(12分)点评:本题考查数列的通项公式的求法,考查数列的前n项和公式的求法,解题时要认真审题,仔细解答,注意错位相减法的合理运用.

练习册系列答案
相关题目