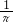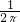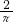Question

将水注入深为4米上口直径为4米的锥形漏斗容器中，注水速度为每秒1立方米，则当水深为2米时，其水面上升的速度为（　　）

• A．

  1

  π

• B．

  1

  2π

• C．

  2

  π

• D．

  3

  π

Answer 1

分析：由已知中漏斗的直径和高相等，先求高度与时间的函数关系式h=(

12t

π

)

1

3

，再利用导数的方法求解，由高度可知时间，从而得解．

解答：解：由已知中漏斗的直径和高相等，
设经过ts水深为h，∴t=

1

12

πh³．
∴h=(

12t

π

)

1

3

．
∴h′=(

12

π

)

1

3

•

1

3

•(t)-

2

3

令h=2，t=

2π

3

∴h′=(

12

π

)

1

3

•

1

3

•(

2π

3

)-

2

3

=

1

π

故选A

点评：本题以旋转体为载体，考查瞬时速度，考查导数的运用，属于基础题．