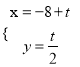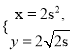题目内容
【题目】已知函数![]() 有极值,且导函数
有极值,且导函数![]() 的极值点是
的极值点是![]() 的零点。(极值点是指函数取极值时对应的自变量的值)
的零点。(极值点是指函数取极值时对应的自变量的值)
求b关于a的函数关系式,并写出定义域;
证明:b>3a;
若![]() ,
, ![]() 这两个函数的所有极值之和不小于
这两个函数的所有极值之和不小于![]() ,求a的取值范围。
,求a的取值范围。
【答案】(1)![]() ,定义域为
,定义域为![]() .(2)见解析(3)
.(2)见解析(3)![]() .
.
【解析】试题分析:(1)先求导函数的极值: ![]() ,再代入原函数得
,再代入原函数得![]() ,化简可得
,化简可得![]() ,根据极值存在条件可得
,根据极值存在条件可得![]() ;(2)由(1)得
;(2)由(1)得![]() ,构造函数
,构造函数![]() ,利用导数研究函数单调性,可得
,利用导数研究函数单调性,可得![]() ,即
,即![]() ;(3)先求证
;(3)先求证![]() 的两个极值之和为零,利用根与系数关系代入化简即得,再研究导函数极值不小于
的两个极值之和为零,利用根与系数关系代入化简即得,再研究导函数极值不小于![]() ,构造差函数
,构造差函数![]() ,利用导数研究其单调性,
,利用导数研究其单调性, ![]() 在
在![]() 上单调递减.而
上单调递减.而![]() ,故可得
,故可得![]() 的取值范围.
的取值范围.
试题解析:解:(1)由![]() ,得
,得![]() .
.
当![]() 时,
时, ![]() 有极小值
有极小值![]() .
.
因为![]() 的极值点是
的极值点是![]() 的零点.
的零点.
所以![]() ,又
,又![]() ,故
,故![]() .
.
因为![]() 有极值,故
有极值,故![]() 有实根,从而
有实根,从而![]() ,即
,即![]() .
.
![]() 时,
时, ![]() ,故
,故![]() 在R上是增函数,
在R上是增函数, ![]() 没有极值;
没有极值;
![]() 时,
时, ![]() 有两个相异的实根
有两个相异的实根![]() ,
, ![]() .
.
列表如下
x |
|
|
|
|
|
| + | 0 | – | 0 | + |
|
| 极大值 |
| 极小值 |
|
故![]() 的极值点是
的极值点是![]() .
.
从而![]() ,
,
因此![]() ,定义域为
,定义域为![]() .
.
(2)由(1)知, ![]() .
.
设![]() ,则
,则![]() .
.
当![]() 时,
时, ![]() ,从而
,从而![]() 在
在![]() 上单调递增.
上单调递增.
因为![]() ,所以
,所以![]() ,故
,故![]() ,即
,即![]() .
.
因此![]() .
.
(3)由(1)知, ![]() 的极值点是
的极值点是![]() ,且
,且![]() ,
, ![]() .
.
从而![]()
![]()
![]()
记![]() ,
, ![]() 所有极值之和为
所有极值之和为![]() ,
,
因为![]() 的极值为
的极值为![]() ,所以
,所以![]() ,
, ![]() .
.
因为![]() ,于是
,于是![]() 在
在![]() 上单调递减.
上单调递减.
因为![]() ,于是
,于是![]() ,故
,故![]() .
.
因此a的取值范围为![]() .
.
点睛:涉及函数的零点问题、方程解的个数问题、函数图象的交点个数问题,一般先通过导数研究函数的单调性、最大值、最小值、变化趋势等,再借助函数的大致图象判断零点、方程根、交点的情况,归根到底还是研究函数的性质,如单调性、极值,然后通过数形结合的思想找到解题的思路.

【题目】某公司2005~2010年的年利润x(单位:百万元)与年广告支出y(单位:百万元)的统计资料如表所示:
年份 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 |
利润x | 12.2 | 14.6 | 16 | 18 | 20.4 | 22.3 |
支出y | 0.62 | 0.74 | 0.81 | 0.89 | 1 | 1.11 |
根据统计资料,则( )
A.利润中位数是16,x与y有正线性相关关系
B.利润中位数是18,x与y有负线性相关关系
C.利润中位数是17,x与y有正线性相关关系
D.利润中位数是17,x与y有负线性相关关系