题目内容
7.对于三次函数f(x)=ax3+bx2+cx+d(a≠0)给出定义:设f′(x)是函数y=f(x)的导数,f''(x)是f′(x)的导数.若方程f''(x)=0有实数解x0,则该点(x0,f(x0))为函数y=f(x)的“拐点”.某同学经过探究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且“拐点”就是对称中心.若$f(x)=\frac{1}{3}{x^3}-\frac{1}{2}{x^2}+3x-\frac{5}{12}$请你根据这一发现,
(1)求函数$f(x)=\frac{1}{3}{x^3}-\frac{1}{2}{x^2}+3x-\frac{5}{12}$的对称中心;
(2)计算$f(\frac{1}{2017})+f(\frac{2}{2017})+f(\frac{3}{2017})+…+f(\frac{2016}{2017})$的值.
分析 (1)由题意对已知函数求两次导数可得图象关于点($\frac{1}{2}$,1)对称,(2)由(1)得:f(x)+f(1-x)=2,即可得到结论.
解答 解:(1)函数的导数f′(x)=x2-x+3,
f″(x)=2x-1,
由f″(x0)=0得2x0-1=0
解得x0=$\frac{1}{2}$,而f($\frac{1}{2}$)=1,
故函数f(x)关于点($\frac{1}{2}$,1)对称,
(2)由(1)得:f(x)+f(1-x)=2,
故设f($\frac{1}{2017}$)+f($\frac{2}{2017}$)+…+f($\frac{2016}{2017}$)=m,
则f($\frac{2016}{2017}$)+f( $\frac{2015}{2017}$)+…+f( $\frac{1}{2017}$)=m,
两式相加得2×2016=2m,
则m=2016.
点评 本题主要考查导数的基本运算,利用条件求出函数的对称中心是解决本题的关键.求和的过程中使用了倒序相加法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.等差数列{an}的前n项和为Sn,若2a6+a7-a9=18,则S6-S3=( )
| A. | 18 | B. | 27 | C. | 36 | D. | 45 |
15.已知直线l过双曲线Γ:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一个焦点且与Γ的一条渐近线平行,若l在y轴上的截距为$\sqrt{6}$a,则双曲线的离心率为( )
| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{6}$ | D. | 2$\sqrt{3}$ |
12.一物体A以速度v(t)=t2-t+6沿直线运动,则当时间由t=1变化到t=4时,物体A运动的路程是( )
| A. | 26.5 | B. | 53 | C. | 31.5 | D. | 63 |
17.若全集U={1,2,3,4,5,6,7},集合A={1,3,5,7},集合B={1,4,7},则集合(∁UA)∩B=( )
| A. | {4} | B. | {1,2,4,6,7} | C. | {3,5} | D. | {1,7} |
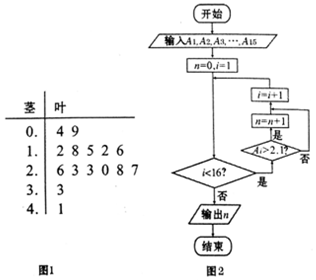 图1是随机抽取的15户居民月均用水量(单位:t)的茎叶图,月均用水量依次记为A1、A2、…A15,图2是统计茎叶图中月均用水量在一定范围内的频数的一个程序框图,那么输出的结果n=7.
图1是随机抽取的15户居民月均用水量(单位:t)的茎叶图,月均用水量依次记为A1、A2、…A15,图2是统计茎叶图中月均用水量在一定范围内的频数的一个程序框图,那么输出的结果n=7.