题目内容

证明：对于任意向量a，b都有||a|-|b||≤|a-b|≤|a|+|b|,并指出等号成立的条件.

思路分析：这是一个涉及两个向量的重要不等式，证明的关键在于正确分类，逐一解决.

证明:（1）当a,b共线时，

①a,b(a,b非零)同向时，则|a-b|=||a|-|b||＜|a|+|b|;  ②只有当a，b中至少有一个零时，|a-b|=||a|-|b||=|a|+|b|;  ③当a，b（a,b非零）反向时，|a-b|=|a|+|b|＞||a|-|b||.

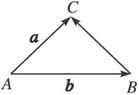
（2）当a，b不共线时，如右上图，在△ABC中，=a,=b,则=-=a-b.

根据三角形中任意两边之差总小于第三边，两边之和总大于第三边可得：

||a|-|b||＜|a-b|＜|a|+|b|.

综合（1）（2）可得：对任意向量a,b都有||a|-|b||≤|a-b|≤|a|+|b|.

只有当a,b同向或a,b中至少一个为0时，||a|-|b||≤|a-b|中的等号成立；只有当a，b反向或a,b中至少一个为0时，|a-b|≤|a|+|b|中的等号成立.

练习册系列答案
相关题目
已知向量
u
=(x，y)与向量
v
=(y，2y-x)的对应关系可用
v
=f(
u
)表示．
（1）设
a
=(1，1)，
b
=(1，0)，求向量f(
a
)及f(
b
)的坐标；
（2）证明：对于任意向量
a
、
b
及常数m、n，恒有f(m
a
+n
b
)=mf(
a
)+nf(
b
)成立；
（3）求使f(
c
)=(3，5)成立的向量
c
．
已知向量
u
=(x，y)与
v
=(y，2y-x)的对应关系用
v
=f(
u
)表示．
（Ⅰ）设
a
=(1，1)，
b
=(1，0)，求向量f(
a
)及f(
b
)的坐标；
（Ⅱ）求使f(
c
)=(p，q)，（p，q为常数）的向量
c
的坐标；
（Ⅲ）证明：对于任意向量
a
，
b
及常数m，n恒有f(m
a
+n
b
)=mf(
a
)+nf(
b
)成立．
已知向量
u
=(x，y)与向量
v
=(y，2y-x)的对应关系可用
v
=f(
u
)表示．
（1）设
a
=(1，1)，
b
=(1，0)，求向量f(
a
)及f(
b
)的坐标；
（2）证明：对于任意向量
a
、
b
及常数m、n，恒有f(m
a
+n
b
)=mf(
a
)+nf(
b
)成立；
（3）求使f(
c
)=(3，5)成立的向量
c
．
已知向量
u
=(x，y)与
v
=(y，2y-x)的对应关系用
v
=f(
u
)表示．
（Ⅰ）设
a
=(1，1)，
b
=(1，0)，求向量f(
a
)及f(
b
)的坐标；
（Ⅱ）求使f(
c
)=(p，q)，（p，q为常数）的向量
c
的坐标；
（Ⅲ）证明：对于任意向量
a
，
b
及常数m，n恒有f(m
a
+n
b
)=mf(
a
)+nf(
b
)成立．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网