题目内容
已知数列 满足:
满足: ,
, (
( )。数列
)。数列 满足
满足
( )。
)。
(1)若 是等差数列,且
是等差数列,且 ,求
,求 的值及
的值及 的通项公式;
的通项公式;
(2)若 是等比数列,求
是等比数列,求 的前
的前 项和
项和
 满足:
满足: ,
, (
( )。数列
)。数列 满足
满足
(
 )。
)。(1)若
 是等差数列,且
是等差数列,且 ,求
,求 的值及
的值及 的通项公式;
的通项公式;(2)若
 是等比数列,求
是等比数列,求 的前
的前 项和
项和
(1)an=n (2)当a=1时,Sn=n;
当a≠1时,Sn= =
=
当a≠1时,Sn=
 =
=
本试题主要考查了数列的通项公式和求和的运用。
解:(1)∵{an}是等差数列,a1=1,a2=a,∴an=1+(n-1)(a-1).
又∵b3=12,∴a3a4=12,即(2a-1)(3a-2)=12,解得a=2或a=- .
.
∵a>0,∴a=2.∴an=n.
(2)∵数列{an}是等比数列,a1=1,a2=a(a>0),∴an=an-1.∴bn=anan+1=a2n-1.
∵ =a2, ∴数列{bn}是首项为a,公比为a2的等比数列.
=a2, ∴数列{bn}是首项为a,公比为a2的等比数列.
当a=1时,Sn=n; 当a≠1时,Sn= =
=
解:(1)∵{an}是等差数列,a1=1,a2=a,∴an=1+(n-1)(a-1).
又∵b3=12,∴a3a4=12,即(2a-1)(3a-2)=12,解得a=2或a=-
 .
.∵a>0,∴a=2.∴an=n.
(2)∵数列{an}是等比数列,a1=1,a2=a(a>0),∴an=an-1.∴bn=anan+1=a2n-1.
∵
 =a2, ∴数列{bn}是首项为a,公比为a2的等比数列.
=a2, ∴数列{bn}是首项为a,公比为a2的等比数列.当a=1时,Sn=n; 当a≠1时,Sn=
 =
=

练习册系列答案
相关题目
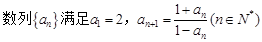 ,则该数列的前2011项的乘积
,则该数列的前2011项的乘积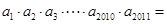 _____________
_____________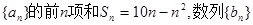 的每一项都有
的每一项都有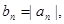 求数列
求数列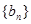 的前n项和
的前n项和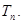
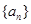 的前n项和为
的前n项和为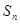 ,且
,且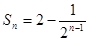 ,数列
,数列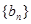 为等差数列,且
为等差数列,且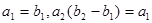 .
. ,求数列
,求数列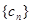 的前n项和
的前n项和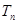 .
.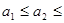 …
…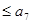 ,其中
,其中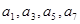 成公比为
成公比为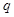 的等比数列,
的等比数列,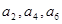 成公差为1的等差数列,则
成公差为1的等差数列,则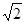
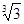
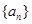 满足
满足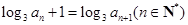 且
且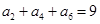 ,则
,则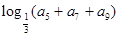 的值是 ( )
的值是 ( )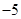
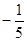
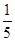
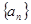 中,
中, 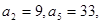 则
则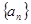 中,有
中,有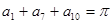 ,则
,则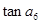 = ▲ 。
= ▲ 。