题目内容
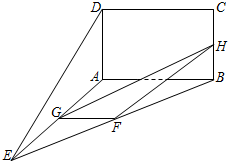 (2011•宁德模拟)如图,矩形ABCD所在的平面与平面AEB垂直,且∠BAE=120°,AE=AB=4,AD=2,F,G,H分别为BE,AE,BC的中点.
(2011•宁德模拟)如图,矩形ABCD所在的平面与平面AEB垂直,且∠BAE=120°,AE=AB=4,AD=2,F,G,H分别为BE,AE,BC的中点.(Ⅰ) 求证:直线DE与平面FGH平行;
(Ⅱ)若点P在直线GF上,且二面角D-BP-A的大小为
| π | 4 |
分析:(Ⅰ)要证明线与面平行,可以先找线与线平行,即在平面FGH内找一条直线与直线DE平行,故取AD得中点M,连接GM即可
(Ⅱ)建立空间直角坐标系,写出相关点的坐标,利用法向量表示二面角的大小,特别注意利用点P在直线GF上的特点,设出动点P的坐标.
(Ⅱ)建立空间直角坐标系,写出相关点的坐标,利用法向量表示二面角的大小,特别注意利用点P在直线GF上的特点,设出动点P的坐标.
解答:解:(Ⅰ)证明:取AD的中点M,连接MH,MG.
∵G,H,F分别是AE,BC,BE的中点,
∴MH∥AB,GF∥AB,
∴MH∥GF,即GFHM四点共面
又由M,G是中点,可得MG∥DE
因为DE?平面MGFH,MG?平面MGFH,
∴DE∥平面MGFH,即直线DE与平面FGH平行.
(Ⅱ)解:如图,在平面ABE内,过A作AB的垂线,记为AP,则AP⊥平面ABCD.
以A为原点,AP、AB、AD所在的直线分别为x轴,y轴,z轴建立建立空间直角坐标系A-xyz.A(0 ,0 ,0) ,B(0 ,4 ,0) ,D(0 ,0 ,2) ,E(2
,-2,0) ,G(
,-1,0),F(
,1,0).
∴
=(0 ,2 ,0),
=(0 ,-4,2),
=(
,-5,0).
设
=λ
=(0 ,2λ ,0),则
=
+
=(
,2λ-5,0).
设平面PBD的法向量为
1=(x,y,z),
则
∴
取y=
,得z=2
,x=5-2λ,
∴
1=(5-2λ ,
,2
).
又平面ABP的法向量为
2=(0,0,1),
∴cos?
1,
2>=
=
=
解得λ=1或4.
故
=
或
=4
∴P(
,1,0)或P(
,7,0)

∵G,H,F分别是AE,BC,BE的中点,
∴MH∥AB,GF∥AB,
∴MH∥GF,即GFHM四点共面
又由M,G是中点,可得MG∥DE
因为DE?平面MGFH,MG?平面MGFH,
∴DE∥平面MGFH,即直线DE与平面FGH平行.
(Ⅱ)解:如图,在平面ABE内,过A作AB的垂线,记为AP,则AP⊥平面ABCD.
以A为原点,AP、AB、AD所在的直线分别为x轴,y轴,z轴建立建立空间直角坐标系A-xyz.A(0 ,0 ,0) ,B(0 ,4 ,0) ,D(0 ,0 ,2) ,E(2
| 3 |
| 3 |
| 3 |
∴
| GF |
| BD |
| BG |
| 3 |
设
| GP |
| GF |
| BP |
| BG |
| GP |
| 3 |
设平面PBD的法向量为
| n |
则
|
|
取y=
| 3 |
| 3 |
∴
| n |
| 3 |
| 3 |
又平面ABP的法向量为
| n |
∴cos?
| n |
| n |
n1•
| ||||
|
|
2
| ||
|
| ||
| 2 |
解得λ=1或4.
故
| GP |
| GF |
| GP |
| GF |
∴P(
| 3 |
| 3 |
点评:本题主要考查直线与直线、直线与平面、平面与平面的位置关系等基础知识,考查空间想象能力、推理论证能力和运算求解能力,考查数形结合思想、化归与转化思想.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
