题目内容
抛物线y=-x2上的点到直线y=-2x+4的最近距离为___________,此点坐标为___________.
(1,-1)
解析：先求出与直线y=-2x+4平行且与抛物线y=-x2相切的直线方程l,设l的方程为y=-2x+b,则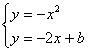
(☆)
x2-2x+b=0,Δ=0,
∴b=1.∴l方程为y=-2x+1,很明显两平行直线间距离d=
=
就是抛物线y=-x2到直线y=-2x+4的最近距离,切点坐标就是所求点坐标,易求方程组(☆)的解
即点(1,-1)为切点坐标.
练习册系列答案
教学练新同步练习系列答案
课前课后同步练习系列答案
课堂小作业系列答案
黄冈小状元口算速算练习册系列答案
成功训练计划系列答案
倍速训练法直通中考考点系列答案
相关题目
抛物线y=x2上的点到直线4x-3y-8=0的距离的最小值是（ ）
A、
| ||
B、
| ||
C、
| ||
| D、3 |