ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΡ≥―ß–Θ―–ΨΩ–‘―ßœΑ–ΓΉιΕ‘ΗΟ–ΘΗΏ»ΐ―ß…ζ ”ΝΠ«ιΩωΫχ––Βς≤ιΘ§‘ΎΗΏ»ΐΒΡ»ΪΧε![]() Οϊ―ß…ζ÷–ΥφΜζ≥ι»ΓΝΥ
Οϊ―ß…ζ÷–ΥφΜζ≥ι»ΓΝΥ![]() Οϊ―ß…ζΒΡΧεΦλ±μΘ§≤ΔΒΟΒΫ»γΆΦΒΡΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΘ°
Οϊ―ß…ζΒΡΧεΦλ±μΘ§≤ΔΒΟΒΫ»γΆΦΒΡΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΘ°
ΡξΦΕΟϊ¥Έ «ΖώΫϋ ” |
|
|
Ϋϋ ” |
|
|
≤ΜΫϋ ” |
|
|
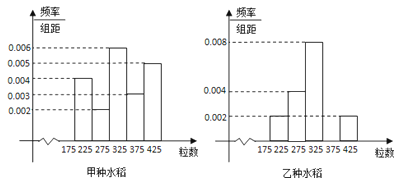
Θ®1Θ©»τ÷±ΖΫΆΦ÷–ΚσΥΡΉιΒΡΤΒ ΐ≥…Β»≤ν ΐΝ–Θ§ ‘ΙάΦΤ»ΪΡξΦΕ ”ΝΠ‘Ύ![]() “‘œ¬ΒΡ»Υ ΐΘΜ
“‘œ¬ΒΡ»Υ ΐΘΜ
Θ®2Θ©―ßœΑ–ΓΉι≥…‘±ΖΔœ÷Θ§―ßœΑ≥…Φ®ΆΜ≥ωΒΡ―ß…ζΘ§Ϋϋ ”ΒΡ±»ΫœΕύΘ§ΈΣΝΥ―–ΨΩ―ß…ζΒΡ ”ΝΠ”κ―ßœΑ≥…Φ® «Ζώ”–ΙΊœΒΘ§Ε‘ΡξΦΕΟϊ¥Έ‘Ύ![]() ΟϊΚΆ
ΟϊΚΆ![]() ΟϊΒΡ―ß…ζΫχ––ΝΥΒς≤ιΘ§ΒΟΒΫ”“±μ÷– ΐΨίΘ§ΗυΨί±μ÷–ΒΡ ΐΨίΘ§ΡήΖώ‘ΎΖΗ¥μΒΡΗ≈¬ ≤Μ≥§Ιΐ
ΟϊΒΡ―ß…ζΫχ––ΝΥΒς≤ιΘ§ΒΟΒΫ”“±μ÷– ΐΨίΘ§ΗυΨί±μ÷–ΒΡ ΐΨίΘ§ΡήΖώ‘ΎΖΗ¥μΒΡΗ≈¬ ≤Μ≥§Ιΐ![]() ΒΡ«ΑΧαœ¬»œΈΣ ”ΝΠ”κ―ßœΑ≥…Φ®”–ΙΊœΒ?
ΒΡ«ΑΧαœ¬»œΈΣ ”ΝΠ”κ―ßœΑ≥…Φ®”–ΙΊœΒ?
Θ®3Θ©‘ΎΘ®ΔρΘ©÷–Βς≤ιΒΡ![]() Οϊ―ß…ζ÷–Θ§Α¥’’Ζ÷≤ψ≥ι―υ‘Ύ≤ΜΫϋ ”ΒΡ―ß…ζ÷–≥ι»ΓΝΥ
Οϊ―ß…ζ÷–Θ§Α¥’’Ζ÷≤ψ≥ι―υ‘Ύ≤ΜΫϋ ”ΒΡ―ß…ζ÷–≥ι»ΓΝΥ![]() »ΥΘ§Ϋχ“Μ≤ΫΒς≤ιΥϊΟ«ΝΦΚΟΒΡΜΛ―έœΑΙΏΘ§≤Δ«“‘Ύ’β
»ΥΘ§Ϋχ“Μ≤ΫΒς≤ιΥϊΟ«ΝΦΚΟΒΡΜΛ―έœΑΙΏΘ§≤Δ«“‘Ύ’β![]() »Υ÷–»Έ»Γ
»Υ÷–»Έ»Γ![]() »ΥΘ§Φ«Οϊ¥Έ‘Ύ
»ΥΘ§Φ«Οϊ¥Έ‘Ύ![]() ΒΡ―ß…ζ»Υ ΐΈΣ
ΒΡ―ß…ζ»Υ ΐΈΣ![]() Θ§«σ
Θ§«σ ΒΡΖ÷≤ΦΝ–ΚΆ ΐ―ßΤΎΆϊΘ°
ΒΡΖ÷≤ΦΝ–ΚΆ ΐ―ßΤΎΆϊΘ°
|
|
|
|
|
|
|
|
|
|
| 7.879 |
![]()
ΗΫΘΚ 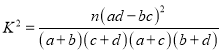
ΓΨ¥πΑΗΓΩ(1)820ΘΜ(2) ‘ΎΖΗ¥μΈσΒΡΗ≈¬ ≤Μ≥§Ιΐ![]() ΒΡ«ΑΧαœ¬»œΈΣ ”ΝΠ”κ―ßœΑ≥…Φ®”–ΙΊœΒΘ°(3)¥πΑΗΦϊΫβΈω.
ΒΡ«ΑΧαœ¬»œΈΣ ”ΝΠ”κ―ßœΑ≥…Φ®”–ΙΊœΒΘ°(3)¥πΑΗΦϊΫβΈω.
ΓΨΫβΈωΓΩ ‘ΧβΖ÷ΈωΘΚ(1)άϊ”Ο÷±ΖΫΆΦ÷–ΒΡ«ΑΦΗΗω ΐΨίΚΆΒ»≤ν ΐΝ–ΒΟΒΫΚσΥΡΉιΒΡΤΒ ΐΘ§‘ΌΙάΦΤΤδΤΒ¬ ΚΆ»Υ ΐΘΜ(2)œ»άϊ”Ο![]() ΙΪ ΫΫχ––«σΫβΘ§‘Όάϊ”ΟΝΌΫγ÷Β±μΫχ––«σΫβΘΜ(3)–¥≥ωΥφΜζ±δΝΩΒΡΥυ”–Ω…Ρή»Γ÷ΒΘ§άϊ”Ο≥§ΦΗΚΈΖ÷≤ΦΒΡΗ≈¬ ΙΪ Ϋ«σ≥ωœύ”ΠΒΡΗ≈¬ Θ§‘ΌΝ–±μΒΟΒΫΖ÷≤ΦΝ–Θ§ΫχΕχ«σ≥ω ΐ―ßΤΎΆϊ .
ΙΪ ΫΫχ––«σΫβΘ§‘Όάϊ”ΟΝΌΫγ÷Β±μΫχ––«σΫβΘΜ(3)–¥≥ωΥφΜζ±δΝΩΒΡΥυ”–Ω…Ρή»Γ÷ΒΘ§άϊ”Ο≥§ΦΗΚΈΖ÷≤ΦΒΡΗ≈¬ ΙΪ Ϋ«σ≥ωœύ”ΠΒΡΗ≈¬ Θ§‘ΌΝ–±μΒΟΒΫΖ÷≤ΦΝ–Θ§ΫχΕχ«σ≥ω ΐ―ßΤΎΆϊ .
‘ΧβΫβΈωΘΚΘ®1Θ©”…÷±ΖΫΆΦΩ…÷ΣΘ§ΒΎ“ΜΉι”–3»ΥΘ§ΒΎΕΰΉι”–7»ΥΘ§ΒΎ»ΐΉι”–27»ΥΘ§
ΓΓ“ρΈΣΚσΥΡΉιΒΡΤΒ ΐ≥…Β»≤ν ΐΝ–Θ§Υυ“‘ΚσΥΡΉιΒΡΤΒ ΐ“ά¥ΈΈΣ27,24,21,18Θ§Υυ“‘ ”ΝΠ
‘Ύ![]() “‘œ¬ΒΡΤΒ¬ ΈΣ
“‘œ¬ΒΡΤΒ¬ ΈΣ![]() Θ§Ι »ΪΡξΦΕ ”ΝΠ‘Ύ
Θ§Ι »ΪΡξΦΕ ”ΝΠ‘Ύ![]() “‘œ¬ΒΡ»Υ ΐ‘ΦΈΣ
“‘œ¬ΒΡ»Υ ΐ‘ΦΈΣ![]() Θ°
Θ°
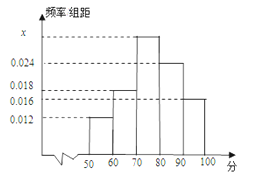
Θ®2Θ©![]() Θ§
Θ§
“ρ¥Υ‘ΎΖΗ¥μΈσΒΡΗ≈¬ ≤Μ≥§Ιΐ![]() ΒΡ«ΑΧαœ¬»œΈΣ ”ΝΠ”κ―ßœΑ≥…Φ®”–ΙΊœΒΘ°
ΒΡ«ΑΧαœ¬»œΈΣ ”ΝΠ”κ―ßœΑ≥…Φ®”–ΙΊœΒΘ°
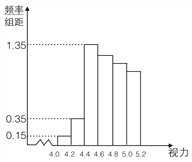
Θ®3Θ©“άΧβ“β9»Υ÷–ΡξΦΕΟϊ¥Έ‘Ύ![]() ΟϊΚΆ
ΟϊΚΆ![]() ΟϊΖ÷±π”–3»ΥΚΆ6»ΥΘ§
ΟϊΖ÷±π”–3»ΥΚΆ6»ΥΘ§
![]() Ω…»Γ0ΓΔ1ΓΔ2ΓΔ3
Ω…»Γ0ΓΔ1ΓΔ2ΓΔ3
ΓΓ ![]() Θ§
Θ§ ![]() Θ§
Θ§
ΓΓ ![]() Θ§
Θ§ ![]()
ΓΓ ![]() ΒΡΖ÷≤ΦΝ–ΈΣ
ΒΡΖ÷≤ΦΝ–ΈΣ
| 0 | 1 | 2 | 3 |
|
|
|
|
|
![]() ΒΡ ΐ―ßΤΎΆϊ
ΒΡ ΐ―ßΤΎΆϊ![]() .
.