Question

【题目】已知函数，其中为自然对数的底数.

（1）函数的图象能否与轴相切？若能与轴相切，求实数的值；否则，请说明理由；

（2）若函数在上单调递增，求实数能取到的最大整数值.

Answer 1

【答案】（1）见解析；（2）1．

【解析】【试题分析】（1）依据题设条件运用导数的几何意义建立方程进行分析求解；（2）依据题设条件借助等比数列的求和公式及等差数列的求和公式进行求解：

（1），

假设函数的图象与轴相切于点，则有，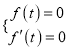

即，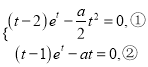

由②可知，代入①中可得．

∵，

∴，即，

∵，

∴方程无解，

故无论取何值，函数的图象都不与轴相切．

（2）记，

由题意知在上恒成立．

由，可得， 的必要条件是，

若，则，

当时， ，故，

下面证明：当时，不等式恒成立．

令，则．

记，则，

当时， 单调递增且；

当时， 单调递减且，

∵．

∴存在唯一的使得，且当时， ， 单调递减；

当时， 单调递增．

∴，

∵，

∴，

∴，

∵，∴，∴，

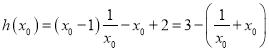从而恒成立，故能取得的最大整数为1．