题目内容
过双曲线 的焦点F作渐近线的垂线l,则直线l与圆O:x2+y2=a2的位置关系是( )
的焦点F作渐近线的垂线l,则直线l与圆O:x2+y2=a2的位置关系是( )A.相交
B.相离
C.相切
D.无法确定
【答案】分析:双曲线 的焦点F(c,0),渐近线y=
的焦点F(c,0),渐近线y= ,由l过焦点F且与渐近线垂直,知直线l的方程是
,由l过焦点F且与渐近线垂直,知直线l的方程是 ,圆O:x2+y2=a2的圆心O(0,0),半径r=a.圆心O(0,0)到直线l的距离d=r,由此知直线l与圆O:x2+y2=a2相切.
,圆O:x2+y2=a2的圆心O(0,0),半径r=a.圆心O(0,0)到直线l的距离d=r,由此知直线l与圆O:x2+y2=a2相切.
解答: 解:双曲线
解:双曲线 的焦点F(c,0),
的焦点F(c,0),
渐近线y= ,
,
∵l过焦点F且与渐近线垂直,
∴直线l的方程是 ,
,
即ax+by-ac=0.
圆O:x2+y2=a2的圆心O(0,0),半径r=a.
∵圆心O(0,0)到直线l的距离d= =
= =a=r.
=a=r.
∴直线l与圆O:x2+y2=a2相切.
故选C.
点评:本题主要考查直线与圆锥曲线的综合应用能力,综合性强,是高考的重点.本题具体涉及到轨迹方程的求法及直线与双曲线的相关知识,圆的简单性质等基础知识.解题时要认真审题,注意点到直线距离公式的灵活运用.
 的焦点F(c,0),渐近线y=
的焦点F(c,0),渐近线y= ,由l过焦点F且与渐近线垂直,知直线l的方程是
,由l过焦点F且与渐近线垂直,知直线l的方程是 ,圆O:x2+y2=a2的圆心O(0,0),半径r=a.圆心O(0,0)到直线l的距离d=r,由此知直线l与圆O:x2+y2=a2相切.
,圆O:x2+y2=a2的圆心O(0,0),半径r=a.圆心O(0,0)到直线l的距离d=r,由此知直线l与圆O:x2+y2=a2相切.解答:
 解:双曲线
解:双曲线 的焦点F(c,0),
的焦点F(c,0),渐近线y=
 ,
,∵l过焦点F且与渐近线垂直,
∴直线l的方程是
 ,
,即ax+by-ac=0.
圆O:x2+y2=a2的圆心O(0,0),半径r=a.
∵圆心O(0,0)到直线l的距离d=
 =
= =a=r.
=a=r.∴直线l与圆O:x2+y2=a2相切.
故选C.
点评:本题主要考查直线与圆锥曲线的综合应用能力,综合性强,是高考的重点.本题具体涉及到轨迹方程的求法及直线与双曲线的相关知识,圆的简单性质等基础知识.解题时要认真审题,注意点到直线距离公式的灵活运用.

练习册系列答案
相关题目
 的一个焦点F作一条渐近的垂线,垂足为点A,与另一条渐近线并于点B,若
的一个焦点F作一条渐近的垂线,垂足为点A,与另一条渐近线并于点B,若 ,则此双曲线的离心率为( )
,则此双曲线的离心率为( )  B.
B. C.2 D.
C.2 D.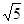
 -
- =1的一个焦点F作一条渐近的垂线,若垂足恰在线段OF(O为原点)的垂直平分线上,则双曲线的离心率为( )
=1的一个焦点F作一条渐近的垂线,若垂足恰在线段OF(O为原点)的垂直平分线上,则双曲线的离心率为( )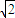
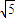

 的一个焦点F作一条渐线的垂线,垂足为点A,与另一条渐近线交于点B,若
的一个焦点F作一条渐线的垂线,垂足为点A,与另一条渐近线交于点B,若 ,则此双曲线的离心率为( )
,则此双曲线的离心率为( )

