题目内容
设常数a>0, 展开式中x3的系数为
展开式中x3的系数为 ,则
,则 =
=
- A.

- B.

- C.2
- D.1
D
分析:利用二项展开式的通项公式求出展开式的通项,令x的指数为3,求出展开式的x3的系数,列出方程求出a,利用等比数列的前n项和公式求出值,再求极限值.
解答: 展开式的通项为
展开式的通项为
令 得r=2
得r=2
展开式中x3的系数为
解得
∴ =
=
故选D
点评:本题考查利用二项展开式的通项公式解决二项展开式的特定项问题、考查等比数列的前n项和公式.
分析:利用二项展开式的通项公式求出展开式的通项,令x的指数为3,求出展开式的x3的系数,列出方程求出a,利用等比数列的前n项和公式求出值,再求极限值.
解答:
 展开式的通项为
展开式的通项为
令
 得r=2
得r=2展开式中x3的系数为

解得

∴
 =
=
故选D
点评:本题考查利用二项展开式的通项公式解决二项展开式的特定项问题、考查等比数列的前n项和公式.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案
相关题目
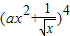 展开式中x3的系数为
展开式中x3的系数为 ,则
,则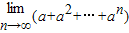 = .
= . 展开式中x3的系数为
展开式中x3的系数为 ,则
,则 = .
= .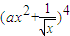 展开式中x3的系数为
展开式中x3的系数为 ,则
,则 = .
= . 展开式中x3的系数为
展开式中x3的系数为 ,则
,则 = .
= .