题目内容
若集合 满足
满足 ,则称
,则称 为集合
为集合 的一种拆分.已知:
的一种拆分.已知:
①当 时,有
时,有 种拆分;
种拆分;
②当 时,有
时,有 种拆分;
种拆分;
③当 时,有
时,有 种拆分;
种拆分;
……
由以上结论,推测出一般结论:当 有_____________种拆分.
有_____________种拆分.
【答案】

【解析】因为当有两个集合时, ;当有三个集合时,
;当有三个集合时, ;当有四个集合时,
;当有四个集合时, ;由此可以归纳当有
;由此可以归纳当有 个集合时,有
个集合时,有 种拆分。
种拆分。

练习册系列答案
相关题目
当一个非空数集 满足条件“如果
满足条件“如果 则
则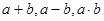
 ,并且当
,并且当 时,
时, ”时,我们就称
”时,我们就称 为一个数域.以下四个关于数域命题:①
为一个数域.以下四个关于数域命题:① 是任何数域的元素;②若数域
是任何数域的元素;②若数域 中有非零元素,则
中有非零元素,则 ;③集合
;③集合 是一个数域;④有理数集是一个数域.其中正确命题的序号为 .
是一个数域;④有理数集是一个数域.其中正确命题的序号为 .
当一个非空数集 满足条件“如果
满足条件“如果 则
则
 ,并且当
,并且当 时,
时, ”时,我们就称
”时,我们就称 为一个数域.以下四个关于数域命题:①
为一个数域.以下四个关于数域命题:① 是任何数域的元素;②若数域
是任何数域的元素;②若数域 中有非零元素,则
中有非零元素,则 ;③集合
;③集合 是一个数域;④有理数集是一个数域.其中正确命题的序号为 .
是一个数域;④有理数集是一个数域.其中正确命题的序号为 .
 为非空数集,若
为非空数集,若 ,都有
,都有 ,则称
,则称 ;
; 为封闭集,且满足
为封闭集,且满足 ,则集合
,则集合 也是封闭集,
也是封闭集,