题目内容
 汽车和自行车分别从A地和C地同时开出,如图,各沿箭头方向(两方向垂直)匀速前进,汽车和自行车的速度分别是10米/秒和5米/秒,已知AC=100米.(汽车开到C地即停止)
汽车和自行车分别从A地和C地同时开出,如图,各沿箭头方向(两方向垂直)匀速前进,汽车和自行车的速度分别是10米/秒和5米/秒,已知AC=100米.(汽车开到C地即停止)(1)经过t秒后,汽车到达B处,自行车到达D处,设B、D间距离为y,写出y关于t的函数关系式,并求出定义域.
(2)经过多少时间后,汽车和自行车之间的距离最短?最短距离是多少?
【答案】分析:(1)经过t小时后,汽车到达B处、自行车到达D处,利用勾股定理可得BD2=BC2+CD2=125[(t-8)2+16],从而可求y关于t的函数关系式,及定义域;
(2)利用配方法求函数的最值,可知当t=8时,汽车和自行车之间的距离最短.
解答:解:(1)经过t小时后,汽车到达B处、自行车到达D处,
则BD2=BC2+CD2=(100-10t)2+(5t)2=125(t2-16t+80)=125[(t-8)2+16]…(4分)
所以 …(6分)
…(6分)
定义域为:t∈[0,10]…(8分)
(2)∵ ,t∈[0,10]
,t∈[0,10]
∴当t=8时, …(12分)
…(12分)
答:经过8秒后,汽车和自行车之间的距离最短.最短距离是 米.…(13分)
米.…(13分)
点评:本题考查的重点是解决实际问题,解题的关键是利用勾股定理构建函数模型,利用配方法解决最值问题,属于中档题.
(2)利用配方法求函数的最值,可知当t=8时,汽车和自行车之间的距离最短.
解答:解:(1)经过t小时后,汽车到达B处、自行车到达D处,
则BD2=BC2+CD2=(100-10t)2+(5t)2=125(t2-16t+80)=125[(t-8)2+16]…(4分)
所以
 …(6分)
…(6分)定义域为:t∈[0,10]…(8分)
(2)∵
 ,t∈[0,10]
,t∈[0,10]∴当t=8时,
 …(12分)
…(12分)答:经过8秒后,汽车和自行车之间的距离最短.最短距离是
 米.…(13分)
米.…(13分)点评:本题考查的重点是解决实际问题,解题的关键是利用勾股定理构建函数模型,利用配方法解决最值问题,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
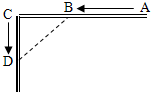 汽车和自行车分别从A地和C地同时开出,如图,各沿箭头方向(两方向垂直)匀速前进,汽车和自行车的速度分别是10米/秒和5米/秒,已知AC=100米.(汽车开到C地即停止)
汽车和自行车分别从A地和C地同时开出,如图,各沿箭头方向(两方向垂直)匀速前进,汽车和自行车的速度分别是10米/秒和5米/秒,已知AC=100米.(汽车开到C地即停止)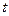 秒后,汽车到达B处,自行车到达D处,设B、D间距离为
秒后,汽车到达B处,自行车到达D处,设B、D间距离为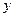 ,写出
,写出
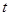 秒后,汽车到达B处,自行车到达D处,设B、D间距离为
秒后,汽车到达B处,自行车到达D处,设B、D间距离为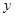 ,写出
,写出
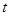 秒后,汽车到达B处,自行车到达D处,设B、D间距离为
秒后,汽车到达B处,自行车到达D处,设B、D间距离为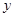 ,写出
,写出
 汽车和自行车分别从A地和C地同时开出,如图,各沿箭头方向(两方向垂直)匀速前进,汽车和自行车的速度分别是10米/秒和5米/秒,已知AC=100米.(汽车开到C地即停止)
汽车和自行车分别从A地和C地同时开出,如图,各沿箭头方向(两方向垂直)匀速前进,汽车和自行车的速度分别是10米/秒和5米/秒,已知AC=100米.(汽车开到C地即停止)