题目内容
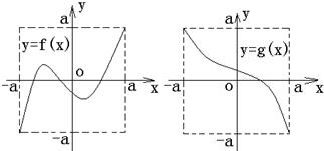10、定义域和值域均为[-a，a]（常数a＞0）的函数y=f（x）和y=g（x）的图象如图所示，给出下列四个命题：（1）方程f[g（x）]=0有且仅有三个解；
（2）方程g[f（x）]=0有且仅有三个解；
（3）方程f[f（x）]=0有且仅有九个解；
（4）方程g[g（x）]=0有且仅有一个解．
那么，其中正确命题的个数是（ ）
分析：通过f（x）=0可知函数有三个解，g（x）=0有一个解，具体分析（1），（2），（3），（4）推出正确结论．
解答：解：（1）方程f[g（x）]=0有且仅有三个解；g（x）有三个不同值，由于y=g（x）是减函数，所以有三个解，正确；
（2）方程g[f（x）]=0有且仅有三个解；从图中可知，f（x）∈（0，a）可能有1，2，3个解，不正确；
（3）方程f[f（x）]=0有且仅有九个解；类似（2）不正确；
（4）方程g[g（x）]=0有且仅有一个解．结合图象，y=g（x）是减函数，故正确．
故选B．
（2）方程g[f（x）]=0有且仅有三个解；从图中可知，f（x）∈（0，a）可能有1，2，3个解，不正确；
（3）方程f[f（x）]=0有且仅有九个解；类似（2）不正确；
（4）方程g[g（x）]=0有且仅有一个解．结合图象，y=g（x）是减函数，故正确．
故选B．
点评：本题考查根的存在性及根的个数判断，函数的图象，考查逻辑思维能力，是基础题．
练习册系列答案
相关题目
若函数f(x)=log2
的定义域和值域均为[1，+∞），则实数a的取值集合为（ ）
| x2+ax+1 |
| x |
| A、{0} |
| B、{a|0≤a≤1} |
| C、{a|a≥0} |
| D、{a|a≥2} |