题目内容
“解方程(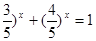 ”有如下思路;设
”有如下思路;设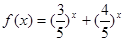 ,则
,则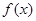 在R上单调递减,且
在R上单调递减,且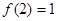 ,故原方程有唯一解x=2,类比上述解题思路,不等式
,故原方程有唯一解x=2,类比上述解题思路,不等式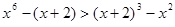 的解集是 .
的解集是 .
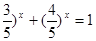 ”有如下思路;设
”有如下思路;设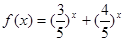 ,则
,则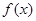 在R上单调递减,且
在R上单调递减,且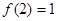 ,故原方程有唯一解x=2,类比上述解题思路,不等式
,故原方程有唯一解x=2,类比上述解题思路,不等式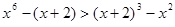 的解集是 .
的解集是 .
试题分析:根据题意,由于“解方程(
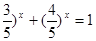 ”有如下思路;设
”有如下思路;设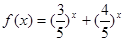 ,则
,则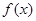 在R上单调递减,且
在R上单调递减,且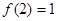 ,故原方程有唯一解x=2,那么对于不等式
,故原方程有唯一解x=2,那么对于不等式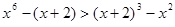 而言,由于
而言,由于 ,当x=2,x=-1函数值为零,那么并且可以判定函数是先减后增再减的,因此可知满足不等式的解集为
,当x=2,x=-1函数值为零,那么并且可以判定函数是先减后增再减的,因此可知满足不等式的解集为
点评:主要是考查了类比推理的思想的运用,来解不等式,属于中档题。

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
 <
< ,1+
,1+ <
< ,1+
,1+ <
< , ,则可归纳出一般式子为( )
, ,则可归纳出一般式子为( ) <
< (n≥2)
(n≥2) (n≥2)
(n≥2) (n≥2)
(n≥2) (n≥2)
(n≥2) 至多有两个解”的假设中,正确的是( )
至多有两个解”的假设中,正确的是( )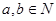 ,若
,若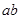 可被5整除,则
可被5整除,则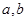 中至少有一个能被5整除”时,反设正确的是( )
中至少有一个能被5整除”时,反设正确的是( ) ,那么
,那么 。
。 ,利用倒序相加法的求和办法,可将
,利用倒序相加法的求和办法,可将 表示成首项
表示成首项 ,末项
,末项 与项数的一个关系式,即
与项数的一个关系式,即 ;类似地,记等比数列
;类似地,记等比数列 项积为
项积为 ,类比等差数列的求和方法,可将
,类比等差数列的求和方法,可将 表示为首项
表示为首项 与项数的一个关系式,即公式
与项数的一个关系式,即公式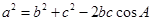 ,把四面体V-BCD与三角形作类比,设二面角V-BC-D,V-CD-B, V-BD-C,C-VB-D,B-VC-D,B-VD-C的大小依次为
,把四面体V-BCD与三角形作类比,设二面角V-BC-D,V-CD-B, V-BD-C,C-VB-D,B-VC-D,B-VD-C的大小依次为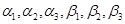 我们可以得到“四面体的余弦定理”:_____________________.(只需写出一个关系式)
我们可以得到“四面体的余弦定理”:_____________________.(只需写出一个关系式) 的不同整数解
的不同整数解 的个数为4 ,
的个数为4 , 的不同整数解
的不同整数解 的不同整数解
的不同整数解 的不同整数解
的不同整数解 ,计算
,计算 ,
, ,推测当
,推测当 时,有_____________.
时,有_____________.