题目内容
 如图,正四面体ABCD的棱长均为a,且AD⊥平面α于A,点B、C、D均在平面α外,且在平面α同一侧,则点B到平面α的距离是( )
如图,正四面体ABCD的棱长均为a,且AD⊥平面α于A,点B、C、D均在平面α外,且在平面α同一侧,则点B到平面α的距离是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:正四面体ABCD的棱长均为a,且AD⊥平面α于A,点B、C、D均在平面α外,且在平面α同一侧,若取AD的中点M,易证AD⊥平面BCM,故平面BCM∥平面α,将求点B到平面α距离的问题转化为两平面间距离的问题求解.
解答:解:取AD的中点M,连接BM、CM,
由于正四面体ABCD,故BM⊥AD,CM⊥AD,
由线面垂直的判定定理知,AD⊥平面BCM,
故平面BCM∥平面α,
∵平面BCM到平面α的距离为
,
∴B到平面α的距离
.
故选A.
由于正四面体ABCD,故BM⊥AD,CM⊥AD,
由线面垂直的判定定理知,AD⊥平面BCM,
故平面BCM∥平面α,
∵平面BCM到平面α的距离为
| a |
| 2 |
∴B到平面α的距离
| a |
| 2 |
故选A.
点评:本题考点是点线面间的距离,考查点到面的距离的求法,本题在求解中将点到面的距离转化为面与面之间的距离,方便了求解.在求点到面的距离问题时,一般直接求得用空间向量或者用体积法求高,也可转化为线到面的距离或者面到面的距离.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
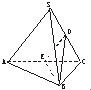 如图,正四面体S-ABC中,D为SC的中点,则BD与SA所成角的余弦值是( )
如图,正四面体S-ABC中,D为SC的中点,则BD与SA所成角的余弦值是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 9、如图,正四面体ABCD的顶点A,B,C分别在两两垂直的三条射线Ox,Oy,Oz上,则在下列命题中,错误的为( )
9、如图,正四面体ABCD的顶点A,B,C分别在两两垂直的三条射线Ox,Oy,Oz上,则在下列命题中,错误的为( ) 14、如图,正四面体ABCD的顶点A、B、C分别在两两垂直的三条射线Ox、Oy、Oz上,给出下列四个命题:
14、如图,正四面体ABCD的顶点A、B、C分别在两两垂直的三条射线Ox、Oy、Oz上,给出下列四个命题: 如图:正四面体S-ABC中,如果E,F分别是SC,AB的中点,那么异面直线EF与SA所成的角等于( )
如图:正四面体S-ABC中,如果E,F分别是SC,AB的中点,那么异面直线EF与SA所成的角等于( ) 如图,正四面体S-ABC的边长为a,D是SA的中点,E是BC的中点,则SDE绕SE旋转一周所得旋转体的体积为
如图,正四面体S-ABC的边长为a,D是SA的中点,E是BC的中点,则SDE绕SE旋转一周所得旋转体的体积为