题目内容
(14分)已知数列 是等差数列,
是等差数列, 为其前
为其前 项和,
项和, ,且
,且 ,
, 成等比数列;
成等比数列;
(1)求数列 的通项公式;
的通项公式;
(2)设 ,
, 为数列
为数列 的前
的前 项和,若
项和,若 对一切正整数
对一切正整数 恒成立,求实数
恒成立,求实数 的范围.
的范围.
【答案】
(1)an="2" n-1;(2) 。
。
【解析】
试题分析:(Ⅰ)设 的公差为
的公差为 ,
, ∴
∴ …2分
…2分
a1,a3,a13成等比数列.则25=(5-2d)(5+10 d),解得d =2,d =0(舍). …4分
an = a3+ (n-3)d=5+(n-3)·2="2" n-1.数列{ an }的通项公式an="2" n-1,n∈N*.………6分
(Ⅱ) ………………7分
………………7分
 则…………………………10分
则…………………………10分

 ……………12分
……………12分
 实数t的取值范围为:
实数t的取值范围为: ……………………………14分
……………………………14分
考点:等差数列的性质;等比数列的性质;通项公式的求法;数列前n项和的求法。
点评:判断数列的单调性,可以用作差法,也可以用做商法。但要注意用做商法的前提条件是数列的每一项都是正的。

练习册系列答案
相关题目
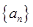 是等差数列,若
是等差数列,若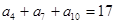 ,
, ,且
,且 ,则
,则 _________.
_________. 是等差数列,
是等差数列, ,则首项
,则首项 .
. 是等差数列,
是等差数列,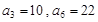 ,数列
,数列 的前n项和是
的前n项和是 ,且
,且 .
. 是等差数列,数列
是等差数列,数列 是等比数列,则
是等比数列,则 的值为 .
的值为 . }是等差数列,且满足:a1+a2+a3=6,a5=5;
}是等差数列,且满足:a1+a2+a3=6,a5=5; }满足:
}满足: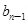 =
= (n≥2,n∈N﹡),b1=1.
(n≥2,n∈N﹡),b1=1. =
= (n∈N﹡),若{
(n∈N﹡),若{ ,求
,求