题目内容
设x=m和x=n是函数f(x)=lnx+
x2-(a+2)x的两个极值点,其中m<n,a∈R.
(Ⅰ) 求f(m)+f(n)的取值范围;
(Ⅱ) 若a≥
+
-2,求f(n)-f(m)的最大值.
注:e是自然对数的底数.
| 1 |
| 2 |
(Ⅰ) 求f(m)+f(n)的取值范围;
(Ⅱ) 若a≥
| e |
| 1 | ||
|
注:e是自然对数的底数.
分析:(Ⅰ)确定函数f(x)的定义域,求导函数,利用极值的运用,建立方程,结合韦达定理,即可求f(m)+f(n)的取值范围;
(Ⅱ)设t=
(t>1),确定t的范围,表示出f(n)-f(m),构造新函数,利用导数法确定函数的单调性,即可求得结论.
(Ⅱ)设t=
| n |
| m |
解答:解:(Ⅰ)函数f(x)的定义域为(0,+∞),f′(x)=
+x-(a+2)=
.
依题意,方程x2-(a+2)x+1=0有两个不等的正根m,n(其中m<n).
故
,∴a>0,
并且m+n=a+2,mn=1.
所以,f(m)+f(n)=lnmn+
(m2+n2)-(a+2)(m+n)
=
[(m+n)2-2mn]-(a+2)(m+n)=-
(a+2)2-1<-3
故f(m)+f(n)的取值范围是(-∞,-3). …(7分)
(Ⅱ)当a≥
+
-2时,(a+2)2≥e+
+2.
若设t=
(t>1),则(a+2)2=(m+n)2=
=t+
+2≥e+
+2.
于是有t+
≥e+
,∴(t-e)(1-
)≥0,∴t≥e
∴f(n)-f(m)=ln
+
(n2-m2)-(a+2)(n-m)=ln
+
(n2-m2)-(n+m)(n-m)
lnt-
(t-
)
构造函数g(t)=lnt-
(t-
)(其中t≥e),则g′(t)=
-
(1+
)=-
<0.
所以g(t)在[e,+∞)上单调递减,g(t)≤g(e)=1-
+
.
故f(n)-f(m)的最大值是1-
+
. …(15分)
| 1 |
| x |
| x2-(a+2)x+1 |
| x |
依题意,方程x2-(a+2)x+1=0有两个不等的正根m,n(其中m<n).
故
|
并且m+n=a+2,mn=1.
所以,f(m)+f(n)=lnmn+
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
故f(m)+f(n)的取值范围是(-∞,-3). …(7分)
(Ⅱ)当a≥
| e |
| 1 | ||
|
| 1 |
| e |
若设t=
| n |
| m |
| (m+n)2 |
| mn |
| 1 |
| t |
| 1 |
| e |
于是有t+
| 1 |
| t |
| 1 |
| e |
| 1 |
| te |
∴f(n)-f(m)=ln
| n |
| m |
| 1 |
| 2 |
| n |
| m |
| 1 |
| 2 |
|
| 1 |
| 2 |
| 1 |
| t |
构造函数g(t)=lnt-
| 1 |
| 2 |
| 1 |
| t |
| 1 |
| t |
| 1 |
| 2 |
| 1 |
| t2 |
| (t-1)2 |
| 2t2 |
所以g(t)在[e,+∞)上单调递减,g(t)≤g(e)=1-
| e |
| 2 |
| 1 |
| 2e |
故f(n)-f(m)的最大值是1-
| e |
| 2 |
| 1 |
| 2e |
点评:本题考查导数知识的运用,考查函数的极值与最值,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
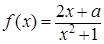 ,函数g(x)=
,函数g(x)= 分别在x=m和x=n处取得极值,且
分别在x=m和x=n处取得极值,且 的值
的值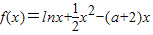 的两个极值点,其中m<n,a∈R.
的两个极值点,其中m<n,a∈R.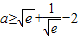 ,求f(n)-f(m)的最大值.
,求f(n)-f(m)的最大值.