题目内容
在多面体ABCDEF中,点O是矩形ABCD的对角线的交点,三角形CDE是等边三角形,棱EF∥BC且EF= BC.
BC.
(1)证明:FO∥平面CDE;
(2)设BC= CD,证明EO⊥平面CDF.
CD,证明EO⊥平面CDF.
 BC.
BC. (1)证明:FO∥平面CDE;
(2)设BC=
 CD,证明EO⊥平面CDF.
CD,证明EO⊥平面CDF.
证明:(1)证明:取CD中点M,连接OM.
在矩形ABCD中,OM∥ BC,且 OM=
BC,且 OM= BC,
BC,
又 EF∥ BC,且 EF=
BC,且 EF= BC,
BC,
则 EF∥OM,EF=OM,
连接EM,于是四边形EFOM为平行四边形.
∴FO∥EM.
又FO不在平面CDE内,且 EM在平面CDE内,
∴FO∥平面CDE.
(2)证明:连接FM,由(1)和已知条件,
在等边△CDE中,CM=DM,EM⊥CD,
且 EM= CD=
CD= BC=EF,
BC=EF,
因此,平行四边形EFOM为菱形,
从而,EO⊥FM,而FM∩CD=M,
∴CD⊥平面EOM,从而CD⊥EO.
而FM∩CD=M,
所以,EO⊥平面CDF.
在矩形ABCD中,OM∥
 BC,且 OM=
BC,且 OM= BC,
BC,又 EF∥
 BC,且 EF=
BC,且 EF= BC,
BC, 则 EF∥OM,EF=OM,
连接EM,于是四边形EFOM为平行四边形.
∴FO∥EM.
又FO不在平面CDE内,且 EM在平面CDE内,
∴FO∥平面CDE.
(2)证明:连接FM,由(1)和已知条件,
在等边△CDE中,CM=DM,EM⊥CD,
且 EM=
 CD=
CD= BC=EF,
BC=EF,因此,平行四边形EFOM为菱形,
从而,EO⊥FM,而FM∩CD=M,
∴CD⊥平面EOM,从而CD⊥EO.
而FM∩CD=M,
所以,EO⊥平面CDF.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
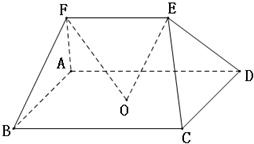 在多面体ABCDEF中,点O是矩形ABCD的对角线的交点,三角形CDE是等边三角形,棱EF∥BC且
在多面体ABCDEF中,点O是矩形ABCD的对角线的交点,三角形CDE是等边三角形,棱EF∥BC且 在多面体ABCDEF中,点O是矩形ABCD的对角线的交点,平面CDE是等边三角形,棱EF∥BC且EF=
在多面体ABCDEF中,点O是矩形ABCD的对角线的交点,平面CDE是等边三角形,棱EF∥BC且EF=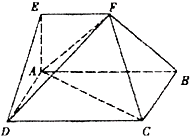 如图,在多面体ABCDEF中,四边形ABCD是矩形,AB∥EF,∠EAB=90°,AB=2,AD=AE=EF=1,平面ABFE⊥平面ABCD.
如图,在多面体ABCDEF中,四边形ABCD是矩形,AB∥EF,∠EAB=90°,AB=2,AD=AE=EF=1,平面ABFE⊥平面ABCD.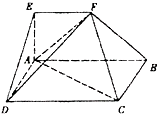 如图,在多面体ABCDEF中,四边形ABCD是矩形,AB∥EF,AB=2EF,∠EAB=90°,平面ABFE⊥平面ABCD.
如图,在多面体ABCDEF中,四边形ABCD是矩形,AB∥EF,AB=2EF,∠EAB=90°,平面ABFE⊥平面ABCD.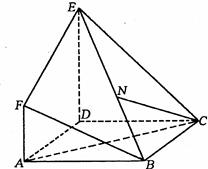 如图,在多面体ABCDEF中,底面ABCD是正方形,AF⊥平面ABCD,DE∥AF,AB=DE=2
如图,在多面体ABCDEF中,底面ABCD是正方形,AF⊥平面ABCD,DE∥AF,AB=DE=2