题目内容
【题目】已知直线l的参数方程为 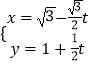 (t为参数),以坐标原点O为极点,以x轴正半轴为极轴,建立极坐标系,圆C的极坐标方程为
(t为参数),以坐标原点O为极点,以x轴正半轴为极轴,建立极坐标系,圆C的极坐标方程为 ![]() .
.
(1)求圆C的直角坐标方程;
(2)若P(x,y)是直线l与圆面 ![]() 的公共点,求
的公共点,求 ![]() 的取值范围.
的取值范围.
【答案】
(1)解:因为圆C的极坐标方程为 ![]() ,
,
所以 ![]()
所以圆C的直角坐标方程 ![]()
(2)解:由圆C的方程 ![]() ,可得
,可得 ![]() ,
,
所以圆C的圆心是 ![]() ,半径是2,
,半径是2,
将 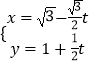 ,代入
,代入 ![]() ,得u=4﹣t,
,得u=4﹣t,
又直线l过 ![]() ,圆C的半径是2,所以﹣2≤t≤2,
,圆C的半径是2,所以﹣2≤t≤2,
即 ![]() 的取值范围是[2,6]
的取值范围是[2,6]
【解析】(Ⅰ)圆C的极坐标方程转化为 ![]() ,由此能求出圆C的直角坐标方程.(Ⅱ)由圆C的方程转化为
,由此能求出圆C的直角坐标方程.(Ⅱ)由圆C的方程转化为 ![]() ,得到圆C的圆心是
,得到圆C的圆心是 ![]() ,半径是2,将
,半径是2,将 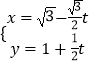 ,代入
,代入 ![]() ,得u=4﹣t,由此能求出
,得u=4﹣t,由此能求出 ![]() 的取值范围.
的取值范围.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目