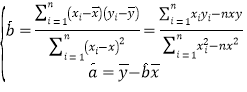题目内容
【题目】已知椭圆![]() ,抛物线
,抛物线![]() 焦点均在x轴上,
焦点均在x轴上,![]() 的中心和
的中心和![]() 顶点均在原点O,从每条曲线上各取两个点,将其坐标记录于表中,则
顶点均在原点O,从每条曲线上各取两个点,将其坐标记录于表中,则![]() 的左焦点到
的左焦点到![]() 的准线之间的距离为( )
的准线之间的距离为( )
| 3 | -2 | 4 |
|
|
| 0 | -4 |
|
A.![]() B.
B.![]() C.1D.2
C.1D.2
【答案】B
【解析】
由题意可知,椭圆和抛物线的方程都是标准方程,由表格中的数据验证可知点![]() 和点
和点![]() 在抛物线上, 两个点
在抛物线上, 两个点![]() 在椭圆
在椭圆![]() 上,由此可求得抛物线和椭圆的方程,再求得抛物线的准线和椭圆的左焦点坐标,从而可得答案.
上,由此可求得抛物线和椭圆的方程,再求得抛物线的准线和椭圆的左焦点坐标,从而可得答案.
由表格中的数据可知,抛物线![]() 的焦点在
的焦点在![]() 轴正半轴上,
轴正半轴上,
设抛物线![]() ,
,
当点![]() 在抛物线上时,可得
在抛物线上时,可得![]() ,解得
,解得![]() ,
,
当点![]() 在抛物线上时,可得
在抛物线上时,可得![]() ,解得
,解得![]() ,
,
当点![]() 在抛物线上时,可得
在抛物线上时,可得![]() ,解得
,解得![]() ,
,
因为这三个点中,有两个点在抛物线上,所以只能是点![]() 和点
和点![]() 在抛物线上,所以
在抛物线上,所以![]() ,所以抛物线
,所以抛物线![]() 的方程为
的方程为![]() ,其准线方程为
,其准线方程为![]() ,
,
所以另外两个点![]() 在椭圆
在椭圆![]() 上,
上,
依题意设椭圆![]() 的方程为
的方程为![]() ,将
,将![]() 代入可得,
代入可得,
![]() ,
, ,解得
,解得![]() ,
,
所以椭圆![]() 的方程为
的方程为![]() ,其左焦点为
,其左焦点为![]() ,
,
所以![]() 的左焦点到
的左焦点到![]() 的准线之间的距离为
的准线之间的距离为![]() ,
,
故选:B.

【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量![]() (吨)与相应的生产能耗
(吨)与相应的生产能耗![]() (吨)标准煤的几组对照数据
(吨)标准煤的几组对照数据
|
|
|
|
|
|
|
|
|
|
(1)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(1)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
参考公式:
【题目】某种设备随着使用年限的增加,每年的维护费相应增加.现对一批该设备进行调查,得到这批设备自购入使用之日起,前5年平均每台设备每年的维护费用大致如表:
年份 |
|
|
|
|
|
维护费 |
|
|
|
|
|
(I)从这![]() 年中随机抽取两年,求平均每台设备每年的维护费用至少有
年中随机抽取两年,求平均每台设备每年的维护费用至少有![]() 年多于
年多于![]() 万元的概率;
万元的概率;
(II)求![]() 关于
关于![]() 的线性回归方程;若该设备的价格是每台
的线性回归方程;若该设备的价格是每台![]() 万元,你认为应该使用满五年换一次设备,还是应该使用满八年换一次设备?并说明理由.
万元,你认为应该使用满五年换一次设备,还是应该使用满八年换一次设备?并说明理由.
参考公式:用最小二乘法求线性回归方程![]() 的系数公式:
的系数公式: