题目内容
已知函数f(x)=mx2+(m-3)x+1的图象与x轴公共点至少有一个在原点右侧.
(1)求实数m的取值范围;
(2)令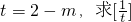 的值;(其中[t]表示不超过t的最大整数,例如:[1]=1,[2.6]=2,[-2.6]=-3)
的值;(其中[t]表示不超过t的最大整数,例如:[1]=1,[2.6]=2,[-2.6]=-3)
(3)对(2)中的t,求函数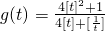 的最小值.
的最小值.
解:(1)当m=0时,f(x)=-3x+1,则-3x+1=0,
得 符合题意…(1分)
符合题意…(1分)
当m<0时,∵f(0)=1,方程f(x)=0有一正一负两个根,符合题意…(2分)
当m>0,则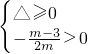 …(2分)
…(2分)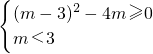 ∴0<m≤1…(2分)
∴0<m≤1…(2分)
综上,得m≤1…(1分)
(2)∵m≤1∴t=2-m≥1…(1分)
若 …(1分)
…(1分)
若 …(1分)
…(1分)
∴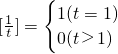 …(1分)
…(1分)
(3)若t=1,则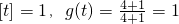 …(1分)
…(1分)
若 …(1分)
…(1分)
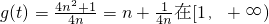 上递增…(2分)
上递增…(2分)
∴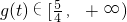 …(1分)
…(1分)
∴g(t)的最小值是1.…(1分)
分析:(1)所给的一元二次方程中二次项的系数时一个字母,要根据字母的取值进行讨论,当m=0,m<0,m>0三种不同的情况进行讨论,得到结果.
(2)根据上一问做出的m的取值,写出t的范围,对t=1,t>1两种情况进行讨论,得到结果是一个分段函数.
(3)根据第二问得到的范围,对所给的函数进行整理,当t>1时,函数是一个递增函数,根据函数的单调性得到函数的值域.
点评:本题考查一元二次方程的根与系数之间的关系和新定义的一个函数的值域的问题,本题解题的关键是理解所给的新定义的函数,做出新定义函数的定义域,本题是一个中档题目.
得
 符合题意…(1分)
符合题意…(1分)当m<0时,∵f(0)=1,方程f(x)=0有一正一负两个根,符合题意…(2分)
当m>0,则
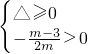 …(2分)
…(2分)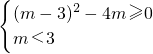 ∴0<m≤1…(2分)
∴0<m≤1…(2分)综上,得m≤1…(1分)
(2)∵m≤1∴t=2-m≥1…(1分)
若
 …(1分)
…(1分)若
 …(1分)
…(1分)∴
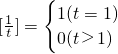 …(1分)
…(1分)(3)若t=1,则
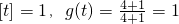 …(1分)
…(1分)若
 …(1分)
…(1分)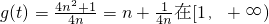 上递增…(2分)
上递增…(2分)∴
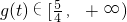 …(1分)
…(1分)∴g(t)的最小值是1.…(1分)
分析:(1)所给的一元二次方程中二次项的系数时一个字母,要根据字母的取值进行讨论,当m=0,m<0,m>0三种不同的情况进行讨论,得到结果.
(2)根据上一问做出的m的取值,写出t的范围,对t=1,t>1两种情况进行讨论,得到结果是一个分段函数.
(3)根据第二问得到的范围,对所给的函数进行整理,当t>1时,函数是一个递增函数,根据函数的单调性得到函数的值域.
点评:本题考查一元二次方程的根与系数之间的关系和新定义的一个函数的值域的问题,本题解题的关键是理解所给的新定义的函数,做出新定义函数的定义域,本题是一个中档题目.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目