题目内容
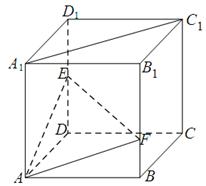
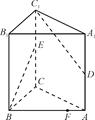
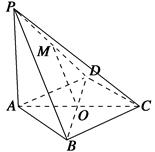
如图,在棱长为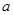 的正方体
的正方体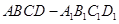 中,点
中,点 是棱
是棱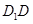 的中点,点
的中点,点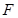 在棱
在棱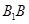 上,且满足
上,且满足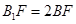 .
.
(1)求证: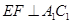 ;
;
(2)在棱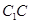 上确定一点
上确定一点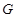 ,使
,使 、
、 、
、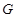 、
、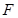 四点共面,并求此时
四点共面,并求此时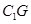 的长;
的长;
(3)求平面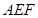 与平面
与平面 所成二面角的余弦值.
所成二面角的余弦值.
(1)详见解析;(2)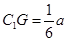 ;(3)
;(3)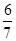 .
.
解析试题分析:本题有两种方法,第一种是传统方法:(1)连接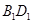 ,先由正方体的性质得到
,先由正方体的性质得到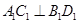 ,以及
,以及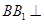 平面
平面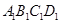 ,从而得到
,从而得到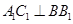 ,利用直线与平面垂直的判定定理可以得到
,利用直线与平面垂直的判定定理可以得到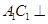 平面
平面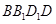 ,于是得到
,于是得到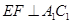 ;(2)假设四点
;(2)假设四点 、
、 、
、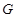 、
、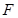 四点共面,利用平面与平面平行的性质定理得到
四点共面,利用平面与平面平行的性质定理得到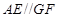 ,
,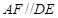 ,于是得到四边形
,于是得到四边形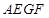 为平行四边形,从而得到
为平行四边形,从而得到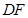 的长度,再结合勾股定理得到
的长度,再结合勾股定理得到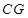 的长度,最终得到
的长度,最终得到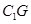 的长度;(3)先延长
的长度;(3)先延长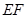 、
、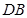 交于点
交于点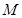 ,连接
,连接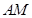 ,找出由平面
,找出由平面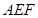 与平面
与平面 所形成的二面角的棱
所形成的二面角的棱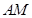 ,借助
,借助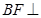 平面
平面 ,从点
,从点 在平面
在平面 内作
内作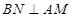 ,连接
,连接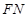 ,利用三垂线法得到
,利用三垂线法得到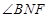 为平面
为平面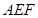 与平面
与平面 所形成的二面角的的平面角,然后在直角
所形成的二面角的的平面角,然后在直角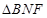 中计算
中计算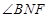 的余弦值;
的余弦值;
第二种方法是空间向量法:(1)以点 为坐标原点,
为坐标原点,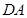 、
、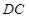 、
、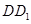 所在直线分别为
所在直线分别为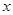 轴、
轴、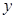 轴、
轴、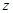 轴建立空间直角坐标系,确定
轴建立空间直角坐标系,确定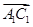 与
与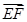 的坐标,利用
的坐标,利用 来证明
来证明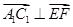 ,进而证明
,进而证明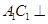
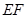 ;(2)先利用平面与平面平行的性质定理得到
;(2)先利用平面与平面平行的性质定理得到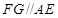 ,然后利用空间向量共线求出点
,然后利用空间向量共线求出点 的坐标,进而求出
的坐标,进而求出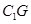 的长度;(3)先求出平面
的长度;(3)先求出平面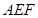 和平面
和平面 的法向量,结合图形得到由平面
的法向量,结合图形得到由平面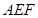 和平面
和平面 所形成的二面角为锐角,最后再利用两个平面的法向量的夹角来进行计算.
所形成的二面角为锐角,最后再利用两个平面的法向量的夹角来进行计算.
试题解析:(1)如下图所示,连接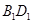 ,
,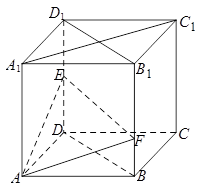
由于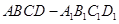 为正方体,所以四边形
为正方体,所以四边形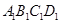 为正方形,所以
为正方形,所以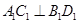 ,
,
且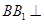 平面
平面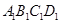 ,
,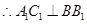 ,
,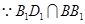 ,
,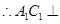 平面
平面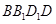 ,
,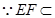 平面
平面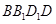 ,
,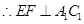 ;
;
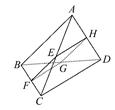
(2)如下图所示,假设 、
、 、
、 、
、

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 A1B1C1,
A1B1C1,
 AB=1,M是PB的中点.
AB=1,M是PB的中点.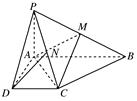

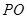 中,已知
中,已知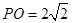 ,
,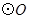 的直径
的直径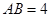 ,点
,点 在底面圆周上,且
在底面圆周上,且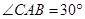 ,
,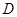 为
为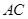 的中点.
的中点.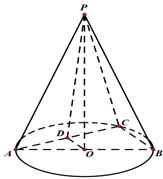
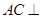 平面
平面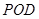 ;
;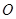 到面
到面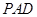 的距离.
的距离.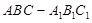 中,
中,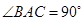 ,
,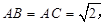
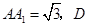 是
是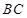 中点,
中点,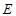 是
是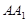 中点.
中点.
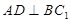 ;
;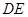 ∥面
∥面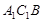 .
.
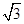 时,求PB的长.
时,求PB的长.