题目内容
【题目】某省的一个气象站观测点在连续4天里记录的![]() 指数
指数![]() 与当天的空气水平可见度
与当天的空气水平可见度![]() (单位:
(单位: ![]() )的情况如表1:
)的情况如表1:
|
| 700 |
|
|
| 0.5 | 3.5 | 6.5 | 9.5 |
该省某市2017年9月![]() 指数频数分布如表2:
指数频数分布如表2:
|
|
|
|
|
|
频数 | 3 | 6 | 12 | 6 | 3 |
(1)设![]() ,根据表1的数据,求出
,根据表1的数据,求出![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)小李在该市开了一家洗车店,经统计,洗车店平均每天的收入与![]() 指数有相关关系,如表3:
指数有相关关系,如表3:
|
|
|
|
|
|
日均收入(元) |
|
|
|
|
|
根据表3估计小李的洗车店9月份平均每天的收入.
(附参考公式: ![]() ,其中
,其中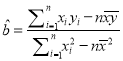 ,
, ![]() )
)
【答案】(1)![]() (2)2400
(2)2400
【解析】试题分析: ![]() 根据表中数据计算平均数与回归系数,即可写出线性回归方程;
根据表中数据计算平均数与回归系数,即可写出线性回归方程;
![]() 根据表
根据表![]() 数据,计算洗车店该月份平均每天的收入值即可。
数据,计算洗车店该月份平均每天的收入值即可。
解析:(1)![]() ,
, ![]()
![]() ,
, ![]()
![]() ,
,
![]() ,
,
∴![]() ,
, ![]() ,
,
所以![]() 关于
关于![]() 的线性回归方程为
的线性回归方程为![]() .
.
根据表3可知,该月30天中有3天每天亏损约2000元,有6天每天亏损约1000元,有12天每天收入约2000元,有6天每天收入约6000元,有3天每天收入约8000元,估计小李的洗车店该月份平均每天的收入约为
![]() 元.
元.

 名校课堂系列答案
名校课堂系列答案【题目】某产品的广告费用x与销售额y的统计数据如下表
广告费用x(万元) | 4 | 2 | 3 | 5 |
销售额y(万元) | 49 | 26 | 39 | 54 |
根据上表可得回归方程 ![]() =
= ![]() x+
x+ ![]() 的
的 ![]() 为9.4,据此模型预报广告费用为6万元时销售额为( )
为9.4,据此模型预报广告费用为6万元时销售额为( )
A.63.6万元
B.65.5万元
C.67.7万元
D.72.0万元
【题目】某同学用“五点法”画函数f(x)=Asin(ωx+φ)(ω>0,|φ|< ![]() )在某一个周期内的图象时,列表并填入了部分数据,如表:
)在某一个周期内的图象时,列表并填入了部分数据,如表:
ωx+φ | 0 |
| π |
| 2π |
x |
|
| |||
Asin(ωx+φ) | 0 | 5 | ﹣5 | 0 |
(1)请将上表数据补充完整,填写在相应位置,并直接写出函数f(x)的解析式;
(2)将y=f(x)图象上所有点向左平行移动θ(θ>0)个单位长度,得到y=g(x)的图象.若y=g(x)图象的一个对称中心为( ![]() ,0),求θ的最小值.
,0),求θ的最小值.