题目内容
已知Sn是公差为d≠0的等差数列{an}的前n项和,{bn}是公比为1-d的等比数列,若b1=a1,b2=a1a2,b3=a2a3,则
=______.
| lim |
| n→∞ |
| Sn | ||
|
由等比数列的定义可得
=
= 1-d,即a2=
=1-d,∴a1+d=1-d,
∴a1=1-2d,a3=2d2-3d+1,∴2(1-d)=(1-2d )+(2d2-3d+1),∴d=
,a1=-2,
∴an=-2+(n-1)
=
n-
,an2=
,
Sn =na1 +
=
,
∴
=
=
=
=
,
答案为
.
| b2 |
| b1 |
| b3 |
| b2 |
| a3 |
| a1 |
∴a1=1-2d,a3=2d2-3d+1,∴2(1-d)=(1-2d )+(2d2-3d+1),∴d=
| 3 |
| 2 |
∴an=-2+(n-1)
| 3 |
| 2 |
| 3 |
| 2 |
| 7 |
| 2 |
| 9n2-42n+49 |
| 4 |
Sn =na1 +
| n(n-1)d |
| 2 |
| 3n2-11n |
| 4 |
∴
| lim |
| n→∞ |
| Sn | ||
|
| lim |
| n→∞ |
| 3n2-11n |
| 9n2-42n+49 |
| lim |
| n→∞ |
3-
| ||||
9-
|
| 3-0 |
| 9-0+0 |
| 1 |
| 3 |
答案为
| 1 |
| 3 |

练习册系列答案
相关题目
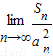 = .
= .