Question

【题目】在△ABC中，内角A，B，C的对边分别为a，b，c，已知asinB＝bsin（A）．

（1）求A；

（2）D是线段BC上的点，若AD＝BD＝2，CD＝3，求△ADC的面积．

Answer 1

【答案】（1）A；（2）.

【解析】

（1）首先利用正弦定理可得asinB＝bsinA，然后利用两角差的正弦公式展开化简即可求解.

（2）设∠B＝θ，，由题意可得∠BAD＝θ，∠ADC＝2θ，∠DACθ，在△ADC中，利用正弦定理可得sinθcosθ，根据同角三角函数的基本关系求出sin2θ，再利用三角形的面积公式即可求解.

（1）由正弦定理可得asinB＝bsinA，

则有bsinA＝b（sinAcosA），化简可得sinAcosA，

可得tanA，

因为A∈（0,π），

所以A．

（2）设∠B＝θ，，由题意可得∠BAD＝θ，∠ADC＝2θ，

∠DACθ，∠ACDθ，

在△ADC中，，则，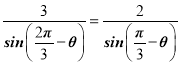

所以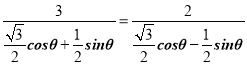，可得sinθcosθ，

又因为sin2θ+cos2θ＝1，可得sinθ，cosθ，

则sin2θ＝2sinθcosθ，

所以S△ADCsin∠ADC．