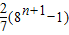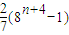题目内容
设f（n）=2+24+27+210+…+23n+10（n∈N），则f（n）等于________．
分析：首先根据题意分析出f（n）是首项为2，公比为8的等比数列的前n+4项和，然后由等比数列前n项和公式求之即可．
解答：由题意知，观察指数1，4，7，…，3n+10
该数列的通项公式为3n-2，而3n+10为数列的第n+4项
∴f（n）是首项为2，公比为8的等比数列的前n+4项和，
所以f（n）=
=
．故答案为：
点评：本题主要考查等比数列的定义及前n项和公式，解决本题的关键是弄清数列的项数，属于易错题．
练习册系列答案
相关题目
设f（n）=2+24+27+210+…+23n+10（n∈N），则f（n）等于（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
（B）
（8n+1-1）
（8n+3-1） （D）
（8n+4-1）
