题目内容
已知向量  =(cosθ,sinθ),
=(cosθ,sinθ), =
=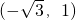 ,
, .
.
(Ⅰ)当  ⊥
⊥ 时,求θ的值;
时,求θ的值;
(Ⅱ)求  •
• 的取值范围.
的取值范围.
解:(Ⅰ)由题意可得  =
= ,…(2分)
,…(2分)
求得 ,由
,由  ,可得 θ=
,可得 θ= . …(6分)
. …(6分)
(Ⅱ)由 =
= …(9分)
…(9分)
∵ ,
,
∴ ,…(10分)
,…(10分)
∴ ,
,
∴ ,…(12分)
,…(12分)
∴-2≤ ≤1,
≤1,
即 •
• 的取值范围 为[-2,1].…(13分)
的取值范围 为[-2,1].…(13分)
分析:(Ⅰ)由题意可得 =
= ,求得
,求得 ,再由θ的范围求得θ的值.
,再由θ的范围求得θ的值.
(Ⅱ)由 =
= ,根据正弦函数的定义域和值域求得
,根据正弦函数的定义域和值域求得 的范围.
的范围.
点评:本题主要考查两个向量的数量积公式的应用,正弦函数的定义域和值域,属于中档题.
 =
= ,…(2分)
,…(2分) 求得
 ,由
,由  ,可得 θ=
,可得 θ= . …(6分)
. …(6分)(Ⅱ)由
 =
= …(9分)
…(9分)∵
 ,
,∴
 ,…(10分)
,…(10分)∴
 ,
,∴
 ,…(12分)
,…(12分)∴-2≤
 ≤1,
≤1,即
 •
• 的取值范围 为[-2,1].…(13分)
的取值范围 为[-2,1].…(13分)分析:(Ⅰ)由题意可得
 =
= ,求得
,求得 ,再由θ的范围求得θ的值.
,再由θ的范围求得θ的值.(Ⅱ)由
 =
= ,根据正弦函数的定义域和值域求得
,根据正弦函数的定义域和值域求得 的范围.
的范围.点评:本题主要考查两个向量的数量积公式的应用,正弦函数的定义域和值域,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知向量
=(cosα,sinα),
=(cosβ,sinβ),若|
-
|=
,则
和
的夹角为( )
| a |
| b |
| a |
| b |
| 2 |
| a |
| b |
| A、60° | B、90° |
| C、120° | D、150° |