Question

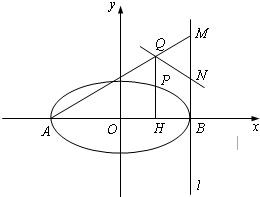如图，已知椭圆C：

x2

a2

+

y2

b2

=1 (a＞b＞0)的长轴AB长为4，离心率e=

3

2

，O为坐标原点，过B的直线l与x轴垂直．P是椭圆上异于A、B的任意一点，PH⊥x轴，H为垂足，延长HP到点Q使得HP=PQ，连接AQ延长交直线l于点M，N为MB的中点．
（1）求椭圆C的方程；
（2）证明Q点在以AB为直径的圆O上；
（3）试判断直线QN与圆O的位置关系．

Answer 1

分析：（1）由题设可得2a=4，

c

a

=

3

2

，由此能导出椭圆C的方程．
（2）设P（x₀，y₀），则

x02

4

+y02=1．由HP=PQ，知Q（x₀，2y₀）．OQ=

x02+(2y02)

=2．所以Q点在以AB为直径的圆O上．
（3）设P（x₀，y₀）（x₀≠±2），则Q（x₀，2y₀），且

x02

4

+y02=1．所以直线AQ的方程为y=

2y0

x0+2

(x+2)．令x=2，得M(2，

8y0

x0+2

)．又B（2，0），N为MB的中点，所以N(2，

4y0

x0+2

)，

OQ

=(x0，2y0)，

NQ

=(x0-2，

2x0y0

x0+2

)．由此能导出直线QN与圆O相切．

解答：解：（1）由题设可得2a=4，

c

a

=

3

2

，
解得a=2，c=

3

，∴b=1．
∴椭圆C的方程为

x2

4

+y2=1．
（2）设P（x₀，y₀），则

x02

4

+y02=1．
∵HP=PQ，∴Q（x₀，2y₀）．∴OQ=

x02+(2y02)

=2．
∴Q点在以O为圆心，2为半径的圆上．即Q点在以AB为直径的圆O上．
（3）设P（x₀，y₀）（x₀≠±2），则Q（x₀，2y₀），且

x02

4

+y02=1．
又A（-2，0），∴直线AQ的方程为y=

2y0

x0+2

(x+2)．
令x=2，得M(2，

8y0

x0+2

)．又B（2，0），N为MB的中点，∴N(2，

4y0

x0+2

)．
∴

OQ

=(x0，2y0)，

NQ

=(x0-2，

2x0y0

x0+2

)．
∴

OQ

•

NQ

=x0(x0-2)+2y0•

2x0y0

x0+2

=x0(x0-2)+

4x0y02

x0+2

=x0(x0-2)+

x0(4-x02)

x0+2

=x₀（x₀-2）+x₀（2-x₀）=0．
∴

OQ

⊥

NQ

．∴直线QN与圆O相切．

点评：本题考查圆锥曲线的性质和应用，解题时要认真审题，仔细解答，注意公式的合理运用．