题目内容
(2013•江西)正项数列{an}的前n项和Sn满足:Sn2-(n2+n-1)Sn-(n2+n)=0
(1)求数列{an}的通项公式an;
(2)令b n=
,数列{bn}的前n项和为Tn.证明:对于任意n∈N*,都有T n<
.
(1)求数列{an}的通项公式an;
(2)令b n=
| n+1 |
| (n+2)2an2 |
| 5 |
| 64 |
分析:(I)由Sn2-(n2+n-1)Sn-(n2+n)=0可求sn,然后利用a1=s1,n≥2时,an=sn-sn-1可求an
(II)由b n=
=
=
[
-
],利用裂项求和可求Tn,利用放缩法即可证明
(II)由b n=
| n+1 |
| (n+2)2an2 |
| n+1 |
| (n+2)2•4n2 |
| 1 |
| 16 |
| 1 |
| n2 |
| 1 |
| (n+2)2 |
解答:解:(I)由Sn2-(n2+n-1)Sn-(n2+n)=0
可得,[sn-(n2+n)](sn+1)=0
∵正项数列{an},sn>0
∴sn=n2+n
于是a1=s1=2
n≥2时,an=sn-sn-1=n2+n-(n-1)2-(n-1)=2n,而n=1时也适合
∴an=2n
(II)证明:由b n=
=
=
[
-
]
∴Tn=
[1-
+
-
+…+
-
+
-
]
=
[1+
-
-
]
<
(1+
)=
可得,[sn-(n2+n)](sn+1)=0
∵正项数列{an},sn>0
∴sn=n2+n
于是a1=s1=2
n≥2时,an=sn-sn-1=n2+n-(n-1)2-(n-1)=2n,而n=1时也适合
∴an=2n
(II)证明:由b n=
| n+1 |
| (n+2)2an2 |
| n+1 |
| (n+2)2•4n2 |
| 1 |
| 16 |
| 1 |
| n2 |
| 1 |
| (n+2)2 |
∴Tn=
| 1 |
| 16 |
| 1 |
| 32 |
| 1 |
| 22 |
| 1 |
| 42 |
| 1 |
| (n-1)2 |
| 1 |
| (n+1)2 |
| 1 |
| n2 |
| 1 |
| (n+2)2 |
=
| 1 |
| 16 |
| 1 |
| 4 |
| 1 |
| (n+1)2 |
| 1 |
| (n+2)2 |
<
| 1 |
| 16 |
| 1 |
| 4 |
| 5 |
| 64 |
点评:本题主要考查了递推公式a1=s1,n≥2时,an=sn-sn-1在求解数列的通项公式中的应用及数列的裂项求和方法的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
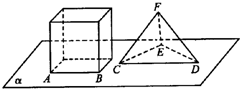 (2013•江西)如果,正方体的底面与正四面体的底面在同一平面α上,且AB∥CD,正方体的六个面所在的平面与直线CE,EF相交的平面个数分别记为m,n,那么m+n=( )
(2013•江西)如果,正方体的底面与正四面体的底面在同一平面α上,且AB∥CD,正方体的六个面所在的平面与直线CE,EF相交的平面个数分别记为m,n,那么m+n=( )