题目内容
设函数f(log4x)=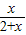 .
.(1)证明:对任意的实数x,都有f(x)+f(1-x)=1;
(2)解不等式:f(x2-2x)+f(4-2x)<1.
【答案】分析:(1)令t=log4x,则 x=4t,由条件求得 f(t)= ,从而求得 f(x)=
,从而求得 f(x)= ,从而证得结论成立.
,从而证得结论成立.
(2)根据f(x)在(-∞,+∞) 上单调递增,不等式f(x2-2x)<1-f(4-2x)利用f(x)+f(1-x)=1可化为f(x2-2x)<f(2x-3),即 x2-2x<2x-3,由此求得它的解集.
解答:解:(1)令t=log4x,则 x=4t,∴f(t)= ,即 f(x)=
,即 f(x)= ,
,
∴f(x)+f(1-x)= +
+ =
= =1,故结论成立.
=1,故结论成立.
(2)∵f(x)= =1-
=1- 在(-∞,+∞) 上是单调递增函数,
在(-∞,+∞) 上是单调递增函数,
∴由不等式:f(x2-2x)+f(4-2x)<1可得 f(x2-2x)<1-f(4-2x),再由f(x)+f(1-x)=1可得 f(x2-2x)<f(2x-3).
∴x2-2x<2x-3,解得1<x<3,
故不等式的解集为 (1,3).
点评:本题主要考查对数函数的图象和性质应用,求函数的解析式,一元二次不等式的解法,属于中档题.
 ,从而求得 f(x)=
,从而求得 f(x)= ,从而证得结论成立.
,从而证得结论成立.(2)根据f(x)在(-∞,+∞) 上单调递增,不等式f(x2-2x)<1-f(4-2x)利用f(x)+f(1-x)=1可化为f(x2-2x)<f(2x-3),即 x2-2x<2x-3,由此求得它的解集.
解答:解:(1)令t=log4x,则 x=4t,∴f(t)=
 ,即 f(x)=
,即 f(x)= ,
,∴f(x)+f(1-x)=
 +
+ =
= =1,故结论成立.
=1,故结论成立.(2)∵f(x)=
 =1-
=1- 在(-∞,+∞) 上是单调递增函数,
在(-∞,+∞) 上是单调递增函数,∴由不等式:f(x2-2x)+f(4-2x)<1可得 f(x2-2x)<1-f(4-2x),再由f(x)+f(1-x)=1可得 f(x2-2x)<f(2x-3).
∴x2-2x<2x-3,解得1<x<3,
故不等式的解集为 (1,3).
点评:本题主要考查对数函数的图象和性质应用,求函数的解析式,一元二次不等式的解法,属于中档题.

练习册系列答案
相关题目
 .
.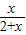 .
.