题目内容
已知A
.B
,其中α、β为锐角,且|AB|=
.
(1)求cos(α-β)的值;
(2)若tan
=
,求cosα及cosβ的值.
|
|
| ||
| 5 |
(1)求cos(α-β)的值;
(2)若tan
| α |
| 2 |
| 1 |
| 2 |
分析:(1)根据向量模的公式建立关于α、β的等式,利用同角三角函数的关系算出cosα•cosβ+sinα•sinβ=
,进而可得cos(α-β)的值;
(2)利用二倍角的余弦公式与同角三角函数的商数关系,算出cosα=
=
,从而得出sinα=
,再进行配角:β=α-(α-β),由两角差的余弦公式加以计算,即可得到cosβ的值.
| 4 |
| 5 |
(2)利用二倍角的余弦公式与同角三角函数的商数关系,算出cosα=
1-tan2
| ||
1+tan2
|
| 3 |
| 5 |
| 4 |
| 5 |
解答:解:(1)∵A
,B
,|AB|=
,
∴
=
,
平方整理,得2-2(cosα•cosβ+sinα•sinβ)=
,
解得cosα•cosβ+sinα•sinβ=
因此,cos(α-β)=
;
(2)∵tan
=
,
∴cosα=cos2
-sin2
=
=
=
=
.
∵α为锐角,∴sinα=
=
,
又∵α-β∈(-
,
),∴sin(α-β)=±
=±
,
①当sin(α-β)=
时,cosβ=cos[α-(α-β)]=cosα•cos(α-β)+sinα•sin(α-β)=
.
②当sin(α-β)=-
时,cosβ=cos[α-(α-β)]=cosα•cos(α-β)+sinα•sin(α-β)=0.
又∵β为锐角,
∴cosβ=0不符合题意,舍去.
因此可得cosβ的值为
.
|
|
| ||
| 5 |
∴
| (cosα-cosβ)2+(sinα-sinβ)2 |
| ||
| 5 |
平方整理,得2-2(cosα•cosβ+sinα•sinβ)=
| 2 |
| 5 |
解得cosα•cosβ+sinα•sinβ=
| 4 |
| 5 |
因此,cos(α-β)=
| 4 |
| 5 |
(2)∵tan
| α |
| 2 |
| 1 |
| 2 |
∴cosα=cos2
| α |
| 2 |
| α |
| 2 |
cos2
| ||||
cos2
|
1-tan2
| ||
1+tan2
|
1-
| ||
1+
|
| 3 |
| 5 |
∵α为锐角,∴sinα=
| 1-cos 2α |
| 4 |
| 5 |
又∵α-β∈(-
| π |
| 2 |
| π |
| 2 |
| -cos2(α-β) |
| 3 |
| 5 |
①当sin(α-β)=
| 3 |
| 5 |
| 24 |
| 25 |
②当sin(α-β)=-
| 3 |
| 5 |
又∵β为锐角,
∴cosβ=0不符合题意,舍去.
因此可得cosβ的值为
| 24 |
| 25 |
点评:本题着重考查了向量模的计算公式、两角和与差的余弦公式、同角三角函数的基本关系与二倍角的三角函数公式等知识,属于中档题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
已知f(x)=sin(2x+
),g(x)=cos(2x-
),则下列结论中不正确的是( )
| π |
| 2 |
| π |
| 2 |
A、将函数f(x)的图象向右平移
| ||
B、函数y=f(x)•g(x)的图象关于(
| ||
C、函数y=f(x)•g(x)的最大值为
| ||
D、函数y=f(x)•g(x)的最小正周期为
|
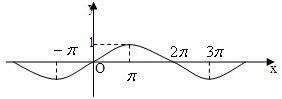 已知函数y=sinωx(ω>0)在一个周期内的图象如图所示,要得到函数y=sin(
已知函数y=sinωx(ω>0)在一个周期内的图象如图所示,要得到函数y=sin(| 1 |
| 2 |
| π |
| 12 |
A、向右平移
| ||
B、向左平移
| ||
C、向右平移
| ||
D、向左平移
|
