题目内容
已知ABCD是边长为2的正方形，E为CD的中点，则
•
= ．
| AD |
| BE |
分析：由已知条件知
•
=
•
=|
|•|
|•cos∠CBE，由此能求出结果．
| AD |
| BE |
| BC |
| BE |
| BC |
| BE |
解答：解：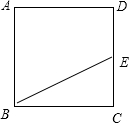
∵ABCD是边长为2的正方形，E为CD的中点，
∴CE=1，BC=2，BE=
=
，
∴cos∠CBE=
=
，
∴
•
=
•
=|
|•|
|•cos∠CBE
=2×
×
=4．
故答案为：4．
∵ABCD是边长为2的正方形，E为CD的中点，∴CE=1，BC=2，BE=
| 1+4 |
| 5 |
∴cos∠CBE=
| 2 | ||
|
2
| ||
| 5 |
∴
| AD |
| BE |
| BC |
| BE |
=|
| BC |
| BE |
=2×
| 5 |
2
| ||
| 5 |
=4．
故答案为：4．
点评：本题考查向量的数量积的计算，是基础题，解题时要注意数形结合法的合理运用．
练习册系列答案
阅读快车系列答案
相关题目
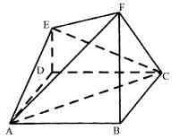如图，已知ABCD是边长为2的正方形，DE⊥平面ABCD，BF⊥平面ABCD，且FB=2DE=2．
如图，已知ABCD是边长为a的正方形，E，F分别是AB，AD的中点，CG⊥面ABCD，CG=a．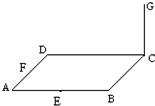
已知ABCD是边长为4的正方形，E、F分别是AB、AD的中点，GC垂直于ABCD所在的平面，且GC=2．求点B到平面EFG的距离．
如图，已知ABCD是边长为2的正方形，DE⊥平面ABCD，BF⊥平面ABCD，且FB=2DE=2．