题目内容
甲、乙两人在罚球线投球命中的概率分别为 与
与 ,且各次投球相互之间没有影响.
,且各次投球相互之间没有影响.
(1)甲、乙两人在罚球线各投球一次,求这二次投球中恰好命中一次的概率;
(2)甲、乙两人在罚球线各投球二次,求这四次投球中至少有一次命中的概率.
解:(1)依题意,记“甲投一次命中”为事件A,“乙投一次命中”为事B,
则P(A)= ,P(B)=
,P(B)= ,P(
,P( )=
)= ,P(
,P( )=
)= .
.
甲、乙两人在罚球线各投球一次,恰好命中一次的事件为
P( )=
)=
答:甲、乙两人在罚球线各投球一次,求恰好命中一次的概率为
(2)∵事件“甲、乙两人在罚球线各投球二次全不命中”的概率是
P′=
∴甲、乙两人在罚球线各投球二次,至少有一次命中的概率为
P=1-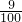 =
=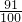
答:甲、乙两人在罚球线各投球二次,至少有一次命中的概率为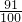
分析:(1)两次投球恰好命中一次包括两种情况,即甲能够命中而乙不能命中,或甲不能命中而乙能够命中,这两种情况是互斥的.根据相互独立事件和互斥事件的概率公式得到结果.
(2)四次投球中至少有一次命中的对立事件是四次投球一次也不能命中,首先根据相互独立事件同时发生的概率做出一次也不能命中的概率,再用对立事件的概率公式得到结果.
点评:本题看出相互独立事件同时发生的概率和对立事件的概率,本题解题的关键是看清题目中所求的事件的概率的意义,正面来解释比较困难,可以选择应用对立事件来解决.
则P(A)=
 ,P(B)=
,P(B)= ,P(
,P( )=
)= ,P(
,P( )=
)= .
.甲、乙两人在罚球线各投球一次,恰好命中一次的事件为

P(
 )=
)=
答:甲、乙两人在罚球线各投球一次,求恰好命中一次的概率为

(2)∵事件“甲、乙两人在罚球线各投球二次全不命中”的概率是
P′=

∴甲、乙两人在罚球线各投球二次,至少有一次命中的概率为
P=1-
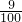 =
=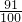
答:甲、乙两人在罚球线各投球二次,至少有一次命中的概率为
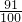
分析:(1)两次投球恰好命中一次包括两种情况,即甲能够命中而乙不能命中,或甲不能命中而乙能够命中,这两种情况是互斥的.根据相互独立事件和互斥事件的概率公式得到结果.
(2)四次投球中至少有一次命中的对立事件是四次投球一次也不能命中,首先根据相互独立事件同时发生的概率做出一次也不能命中的概率,再用对立事件的概率公式得到结果.
点评:本题看出相互独立事件同时发生的概率和对立事件的概率,本题解题的关键是看清题目中所求的事件的概率的意义,正面来解释比较困难,可以选择应用对立事件来解决.

练习册系列答案
相关题目