题目内容
椭圆 关于抛物线y2=-4x的准线l对称的椭圆方程是 .
关于抛物线y2=-4x的准线l对称的椭圆方程是 .
【答案】分析:抛物线y2=-4x的焦点在x轴上,且开口向右,2p=4,由此可得抛物线y2=-4x的准线方程.设椭圆上的点坐标为(x,y),其关于准线的对称点坐标为(x,y),根据对称性可分别表示出x和y,代入椭圆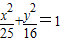 即可得到答案.
即可得到答案.
解答:解:抛物线y2=-4x的焦点在x轴上,且开口向右,2p=4
∴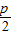 =1
=1
∴抛物线y2=-4x的准线方程为x=1,
设已知椭圆上的点坐标为(x,y),其关于x=1的对称点坐标为(x,y)
依题意可知x=-x+2,y=y
把点(x,y)代入椭圆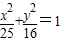 得
得 ,即
,即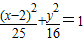 .
.
故答案为: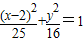 .
.
点评:本题主要考查了抛物线的标准方程、对称变换,代入法求轨迹方程等.解答关键是充分利用了点的对称性来解决问题.
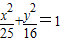 即可得到答案.
即可得到答案.解答:解:抛物线y2=-4x的焦点在x轴上,且开口向右,2p=4
∴
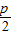 =1
=1∴抛物线y2=-4x的准线方程为x=1,
设已知椭圆上的点坐标为(x,y),其关于x=1的对称点坐标为(x,y)
依题意可知x=-x+2,y=y
把点(x,y)代入椭圆
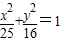 得
得 ,即
,即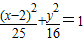 .
.故答案为:
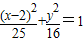 .
.点评:本题主要考查了抛物线的标准方程、对称变换,代入法求轨迹方程等.解答关键是充分利用了点的对称性来解决问题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
 关于抛物线y2=-4x的准线l对称的椭圆方程是________.
关于抛物线y2=-4x的准线l对称的椭圆方程是________.