题目内容
探究函数f（x）=x+
，x∈（0，+∞）的最小值，并确定取得最小值时x的值．列表如下：
| x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
| y | … | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.005 | 4.002 | 4.04 | 4.3 | 5 | 4.8 | 7.57 | … |
（1）函数f（x）=x+
（x＞0）在区间______上递减；并利用单调性定义证明．函数f（x）=x+（x＞0）在区间______上递增．当x=______时，y最小=______．（2）函数f（x）=x+
（x＜0）时，有最值吗？是最大值还是最小值？此时x为何值？（直接回答结果，不需证明）
解：（1）根据表格可知，f（x）=x+（x＞0）在区间（0，2）上单调递减，在（2，+∞）上单调递增，
所以x=2时，f（x）有最小值f（2）=4；
证明如下：
设2＞x2＞x1＞0，则f（x2）-f （x1）=（
）-（
）=
．
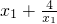∵2＞x2＞x1＞0，∴x2-x1＞0，x1x2-4＜0，
∴f（x2）-f （x1）＜0，即f（x2）＜f（x1）．
∴f（x）在（0，2）上单调递减．
（2）由（1）知，f（x）在（0，2）上单调递减，在（2，+∞）上单调递增，
f（x）在∈（0，+∞）的最小值为f（2）=4，
又f（x）=x+为奇函数，所以x＜0时，f（x）有最大值f（-2）=-4；
故答案为：（1）（0，2）；（2，+∞），2，4；
分析：（1）根据表格可求得函数的单调区间，根据单调性可求得最小值，利用单调性的定义可作出证明；
（2）根据奇函数的性质可作出回答；
点评：本题考查函数单调性的性质及其证明，属中档题．
（x＞0）在区间（0，2）上单调递减，在（2，+∞）上单调递增，所以x=2时，f（x）有最小值f（2）=4；
证明如下：
设2＞x2＞x1＞0，则f（x2）-f （x1）=（
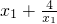）-（）=．∵2＞x2＞x1＞0，∴x2-x1＞0，x1x2-4＜0，
∴f（x2）-f （x1）＜0，即f（x2）＜f（x1）．
∴f（x）在（0，2）上单调递减．
（2）由（1）知，f（x）在（0，2）上单调递减，在（2，+∞）上单调递增，
f（x）在∈（0，+∞）的最小值为f（2）=4，
又f（x）=x+
为奇函数，所以x＜0时，f（x）有最大值f（-2）=-4；故答案为：（1）（0，2）；（2，+∞），2，4；
分析：（1）根据表格可求得函数的单调区间，根据单调性可求得最小值，利用单调性的定义可作出证明；
（2）根据奇函数的性质可作出回答；
点评：本题考查函数单调性的性质及其证明，属中档题．
练习册系列答案
相关题目
探究函数f(x)=x+
，x∈(0，+∞)的最小值，并确定取得最小值时x的值．列表如下：
请观察表中y值随x值变化的特点，完成以下的问题．
（1）函数f(x)=x+
(x＞0)在区间（0，2）上递减，函数f(x)=x+
(x＞0)在区间 上递增；
（2）函数f(x)=x+
(x＞0)，当x= 时，y最小= ；
（3）函数f(x)=x+
(x＜0)时，有最值吗？是最大值还是最小值？此时x为何值？（直接回答结果，不需证明）
| 4 |
| x |
| x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
| y | … | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.005 | 4.002 | 4.04 | 4.3 | 5 | 5.8 | 7.57 | … |
（1）函数f(x)=x+
| 4 |
| x |
| 4 |
| x |
（2）函数f(x)=x+
| 4 |
| x |
（3）函数f(x)=x+
| 4 |
| x |
探究函数f（x）=x+
x∈（0，+∞）的最小值，并确定相应的x的值，列表如下，请观察表中y值随x值变化的特点，完成下列问题：
（1）若当x＞0时，函数f（x）=x+
时，在区间（0，2）上递减，则在 上递增；
（2）当x= 时，f（x）=x+
，x＞0的最小值为 ；
（3）试用定义证明f（x）=x+
，x＞0在区间上（0，2）递减；
（4）函数f（x）=x+
，x＜0有最值吗？是最大值还是最小值？此时x为何值？
解题说明：（1）（2）两题的结果直接填写在答题卷中横线上；（4）题直接回答，不需证明．
| 4 |
| x |
| x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
| y | … | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.005 | 4.102 | 4.24 | 4.3 | 5 | 5.8 | 7.57 | … |
| 4 |
| x |
（2）当x=
| 4 |
| x |
（3）试用定义证明f（x）=x+
| 4 |
| x |
（4）函数f（x）=x+
| 4 |
| x |
解题说明：（1）（2）两题的结果直接填写在答题卷中横线上；（4）题直接回答，不需证明．