Question

【题目】某经销商计划销售一款新型的空气净化器，经市场调研发现以下规律：当每台净化器的利润为 x （单位：元， x 0 ）时，销售量 q(x) （单位：百台）与 x 的关系满足：若 x 不超过 20 ， 则 ；若 x 大于或等于180 ，则销售量为零；当 20 ≤ x ≤180 时，（ a ， b 为实常数）．

（Ⅰ）求函数 q(x) 的表达式；

（Ⅱ）当 x 为多少时，总利润（单位：元）取得最大值，并求出该最大值．

Answer 1

【答案】（1）.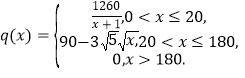

（2）当 x 等于80 元时，总利润取得最大值 240000 元．

【解析】

试题分析：（1）求分段函数解析式，可从分段的节点出发，寻找条件，确定参数：解得列出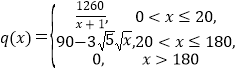（2）先列出利润函数解析式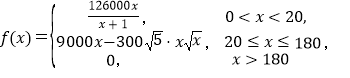，分三段求最值，第一段为分式函数，可利用变量分离，结合单调性求最大值；第二段利用导数求极值点，研究单调趋势，求最大值；第三段为常函数，最后求三段最大值的最大值

试题解析：解：（1）当时，由得

故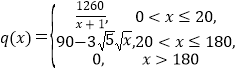

（2）设总利润，

由（1）得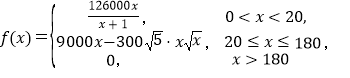

当时，，在上单调递增，

所以当时，有最大值．

当时，，，

令，得．

当时，，单调递增，

当时，，单调递减，

所以当时，有最大值．

当时，﹒

答：当等于元时，总利润取得最大值元．