题目内容
(本小题满分14分)
已知等差数列{an}的前n项和为Sn,a1=1+,S3=9+3
(1)求数列{an}的通项an与前n项和Sn;
(2)设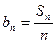 ,求证:数列{bn}中任意不同的三项都不可能成为等比数列.
,求证:数列{bn}中任意不同的三项都不可能成为等比数列.
已知等差数列{an}的前n项和为Sn,a1=1+,S3=9+3
(1)求数列{an}的通项an与前n项和Sn;
(2)设
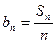 ,求证:数列{bn}中任意不同的三项都不可能成为等比数列.
,求证:数列{bn}中任意不同的三项都不可能成为等比数列.(1)
(2)略

(2)略
解:(1)∵S3=9+3,∴a2=3+,
∴d=2…………………………………2分
∴an= ,………………………4分
,………………………4分
 .…………………6分
.…………………6分
(2)∵ …………………7分
…………………7分
假设数列{bn}存在不同的三项 ,
, ,
, 成等比数列
成等比数列
∴ =
= ,…………………9分
,…………………9分
∴
∴ …………………10分
…………………10分
∴ ,…………………………………12分
,…………………………………12分
∴ ,即
,即 与
与 矛盾,
矛盾,
∴ 数列{bn}中任意不同的三项都不可能成为等比数列.…………………14分
∴d=2…………………………………2分
∴an=
 ,………………………4分
,………………………4分 .…………………6分
.…………………6分(2)∵
 …………………7分
…………………7分假设数列{bn}存在不同的三项
 ,
, ,
, 成等比数列
成等比数列∴
 =
= ,…………………9分
,…………………9分∴

∴
 …………………10分
…………………10分∴
 ,…………………………………12分
,…………………………………12分∴
 ,即
,即 与
与 矛盾,
矛盾,∴ 数列{bn}中任意不同的三项都不可能成为等比数列.…………………14分

练习册系列答案
相关题目
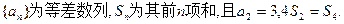
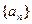 的通项公式; (2)求证数列
的通项公式; (2)求证数列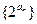 是等比数列;
是等比数列;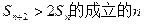 的集合。
的集合。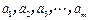 (
(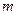 为正整数)满足条件
为正整数)满足条件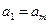 ,
,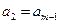 ,…,
,…,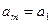 ,即
,即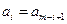 (
(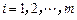 ),我们称其为“对称数列”.
),我们称其为“对称数列”. 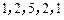 与数列
与数列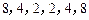 都是“对称数列”.
都是“对称数列”. 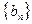 是7项的“对称数列”,其中
是7项的“对称数列”,其中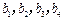 是等差数列,且
是等差数列,且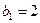 ,
,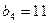 .依次写出
.依次写出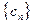 是
是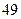 项的“对称数列”,其中
项的“对称数列”,其中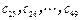 是首项为
是首项为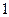 ,公比为
,公比为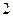 的等比数列,求
的等比数列,求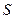 ;
;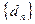 是
是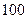 项的“对称数列”,其中
项的“对称数列”,其中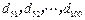 是首项为
是首项为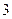 的等差数列.求
的等差数列.求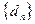 前
前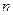 项的和
项的和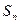
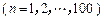 .
. 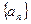 满足:
满足: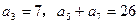 ,
,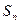 ,
,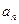 及
及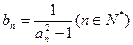 ,求数列
,求数列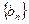 的前n项和
的前n项和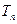 .
. 中有
中有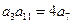 ,数列
,数列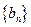 是等差数列,且
是等差数列,且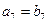 ,则
,则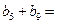 ( )
( ) 是公差不为零的等差数列,且
是公差不为零的等差数列,且 ,则下列四个数列
,则下列四个数列 ; ②
; ② ;
; ; ④
; ④
 的前n项和为
的前n项和为 ,若
,若 ,则
,则 等于( )
等于( )