题目内容
若f(x)=atan4x-bsin32x+cx+7,且f(-1)=0,则f(1)的值等于
______.
令g(x)=atan4x-bsin32x+cx
∵g(-x)=-g(x)
∴g(x)是奇函数
又∵f(-1)=0
即:f(-1)-g(-1)+1=0
∴g(-1)=-1
∴g(1)=-g(-1)=1
∴f(1)=g(1)+1=2
故答案为:2
∵g(-x)=-g(x)
∴g(x)是奇函数
又∵f(-1)=0
即:f(-1)-g(-1)+1=0
∴g(-1)=-1
∴g(1)=-g(-1)=1
∴f(1)=g(1)+1=2
故答案为:2

练习册系列答案
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
 时,
时, 取得最大值;
取得最大值;
 的值域是[-1,1];
的值域是[-1,1];
 是
是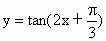 的图象的一个对称中心.
的图象的一个对称中心.
 时,
时, 取得最大值;
取得最大值; 的值域是[-1,1];
的值域是[-1,1]; 是
是 的图象的一个对称中心.
的图象的一个对称中心.