题目内容
某中学号召本校学生在本学期参加市创办卫生城的相关活动,学校团委对该校学生是否关心创卫活动用简单抽样方法调查了 位学生(关心与不关心的各一半),
位学生(关心与不关心的各一半),
结果用二维等高条形图表示,如图.

(1)完成列联表,并判断能否有 ℅的把握认为是否关心创卫活动与性别有关?
℅的把握认为是否关心创卫活动与性别有关?
(参考数据与公式: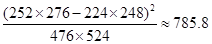
 ;
;
(2)已知校团委有青年志愿者100名,他们已参加活动的情况记录如下:
(i)从志愿者中任选两名学生,求他们参加活动次数恰好相等的概率;
(ii)从志愿者中任选两名学生,用 表示这两人参加活动次数之差的绝对值,求随机变量
表示这两人参加活动次数之差的绝对值,求随机变量 的分布列及数学期望
的分布列及数学期望 .
.
 位学生(关心与不关心的各一半),
位学生(关心与不关心的各一半),结果用二维等高条形图表示,如图.

(1)完成列联表,并判断能否有
 ℅的把握认为是否关心创卫活动与性别有关?
℅的把握认为是否关心创卫活动与性别有关?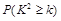 | 0.10 | 0.05 | 0.01 |
 | 2.706 | 3.841 | 6.635 |
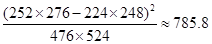
 ;
;| | 女 | 男 | 合计 |
| 关心 | | | 500 |
| 不关心 | | | 500 |
| 合计 | | 524 | 1000 |
(2)已知校团委有青年志愿者100名,他们已参加活动的情况记录如下:
| 参加活动次数 | 1 | 2 | 3 |
| 人数 | 10 | 50 | 40 |
(i)从志愿者中任选两名学生,求他们参加活动次数恰好相等的概率;
(ii)从志愿者中任选两名学生,用
 表示这两人参加活动次数之差的绝对值,求随机变量
表示这两人参加活动次数之差的绝对值,求随机变量 的分布列及数学期望
的分布列及数学期望 .
.(1)不能有 ℅的把握认为是否关心创卫活动与性别有关.
℅的把握认为是否关心创卫活动与性别有关.
(2)(i)他们参加活动次数恰好相等的概率为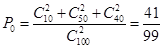
(ii) 分布列为
数学期望: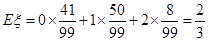 。
。
 ℅的把握认为是否关心创卫活动与性别有关.
℅的把握认为是否关心创卫活动与性别有关. (2)(i)他们参加活动次数恰好相等的概率为
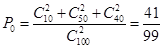
(ii) 分布列为
 | 0 | 1 | 2 |
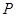 | 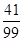 | 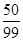 | 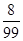 |
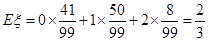 。
。试题分析:(1)作出列联表:
| | 女 | 男 | 合计 |
| 关心 | 252 | 248 | 500 |
| 不关心 | 224 | 276 | 500 |
| 合计 | 476 | 524 | 1000 |
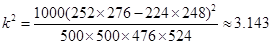
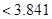 4分
4分所以不能有
 ℅的把握认为是否关心创卫活动与性别有关. 5分
℅的把握认为是否关心创卫活动与性别有关. 5分(2)(i)他们参加活动次数恰好相等的概率为
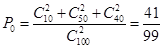 7分
7分(ii) 从志愿者中任选两名学生,记“这两人中一人参加1次活动,另一个参加两次活动”为事件
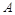 ,“这两人中一人参加2次活动,另一个参加3次活动”为事件
,“这两人中一人参加2次活动,另一个参加3次活动”为事件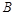 ,“这两人中一人参加1次活动,另一个参加两次活动”, “这两人中一人参加1次活动,另一个参加3次活动”为事件
,“这两人中一人参加1次活动,另一个参加两次活动”, “这两人中一人参加1次活动,另一个参加3次活动”为事件 . 8分
. 8分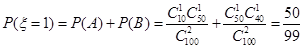 9分
9分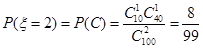 10分
10分分布列为
 | 0 | 1 | 2 |
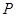 | 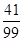 | 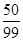 | 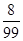 |
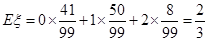 12分
12分点评:典型题,统计中的抽样方法,频率直方图,概率计算及分布列问题,是高考必考内容及题型。古典概型概率的计算问题,关键是明确基本事件数,往往借助于“树图法”,做到不重不漏。本题对计算能力要求较高,难度较大。

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
 名男生和
名男生和




 列联表,并回答能否有90%的把握认为“学生周日上网时间与性别有关”?
列联表,并回答能否有90%的把握认为“学生周日上网时间与性别有关”? ,其中
,其中

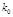
 之间的几组数据如下表:
之间的几组数据如下表:


 求得的直线方程为
求得的直线方程为 则以下结论正确的是( )
则以下结论正确的是( ) B.
B. C.
C. D.
D.

 列联表:已知从全部210人中随机抽取1人为优秀的概率为
列联表:已知从全部210人中随机抽取1人为优秀的概率为 .
. ,若每次抽取的结果是相互独立的,求
,若每次抽取的结果是相互独立的,求 .
.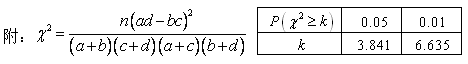
 联表:
联表:
 的把握认为“成绩与班级有关系”
的把握认为“成绩与班级有关系” ,若每次抽取得结果是相互独立的,求
,若每次抽取得结果是相互独立的,求 和方差
和方差


 列联表算得
列联表算得 的观测值
的观测值 ,参照附表:
,参照附表:

 ,则
,则 时,
时, 的估计值为
的估计值为  ,其中甲社区有驾驶员96人.若在甲、乙、丙、丁四个社区抽取驾驶员的人数分别为12,21,25,43,则这四个社区驾驶员的总人数
,其中甲社区有驾驶员96人.若在甲、乙、丙、丁四个社区抽取驾驶员的人数分别为12,21,25,43,则这四个社区驾驶员的总人数