题目内容
(本小题满分7分)选修4—2:矩阵与变换
若二阶矩阵 满足
满足 .
.
(Ⅰ)求二阶矩阵 ;
;
(Ⅱ)把矩阵 所对应的变换作用在曲线
所对应的变换作用在曲线 上,求所得曲线的方程.
上,求所得曲线的方程.
(I) ;(II)
;(II)
【解析】
试题分析:(Ⅰ)记矩阵 ,故
,故 ,故
,故 ,再利用矩阵的乘法可得
,再利用矩阵的乘法可得 ;设二阶矩阵
;设二阶矩阵 所对应的变换为
所对应的变换为 ,得
,得 ,解得
,解得 ,又
,又 得
得
试题解析:(Ⅰ)记矩阵 ,故
,故 ,故
,故 . 2分
. 2分
由已知得 . 3分
. 3分
(Ⅱ)设二阶矩阵 所对应的变换为
所对应的变换为 ,得
,得 ,
,
解得 , 5分
, 5分
又 ,故有
,故有 ,化简得
,化简得 .故所得曲线的方程为
.故所得曲线的方程为 . 7分
. 7分
考点:矩阵与变换

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
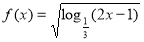 ,则
,则 的定义域为_______________ .
的定义域为_______________ .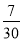 B.
B.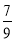 C.
C.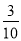 D.
D.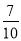
 是奇函数且
是奇函数且 ,当
,当 时,
时,  (
( ),则实数
),则实数 的值为
的值为 B.
B. C.
C. D.
D.
 ,
, ,若任取
,若任取 ,则
,则 的概率为
的概率为 B.
B. C.
C. D.
D.
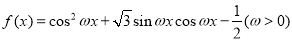 的最小正周期为
的最小正周期为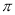 .
.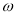 值及
值及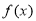 的单调递增区间;
的单调递增区间;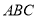 中,
中,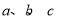 分别是三个内角
分别是三个内角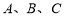 所对边,若
所对边,若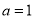 ,
,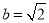 ,
,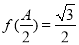 ,求
,求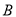 的大小.
的大小. 中,
中, ,
, ,
, ,
, ,则
,则 .
.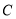 的极坐标方程是
的极坐标方程是 ,以极点为平面直角坐标系的原点,极轴为
,以极点为平面直角坐标系的原点,极轴为 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线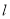 的参数方程是
的参数方程是 (
(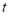 为参数).
为参数).
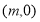 ,若直线
,若直线 两点,且
两点,且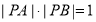 ,求实数
,求实数 的值.
的值.