题目内容
已知函数![]() ,
,![]() .
.
(I)求函数f(x)的解析式;
(II)若对于任意x∈(0,+∞),都有f(x)+g(x)≤a成立,求实数a的取值范围;
(III)设x1,x2>0,a1,a2∈[0,1],且a1+a2=1,求证:![]() .
.
考点:
导数在最大值、最小值问题中的应用;函数单调性的性质;导数的运算;不等式的证明.
专题:
导数的综合应用.
分析:
(I)为了求函数f(x)的解析式,根据题意,即求出其中的f'(2)的值,故只须对函数求导后令x=2即可;
(II)设F(x)=f(x)+g(x),对于任意x∈(0,+∞),都有f(x)+g(x)≤a成立,只须a≥F(x)max即可,利用导数求函数F(x)的最大值,即可得出实数a的取值范围;
(III)由(II),得F(x)=lnx﹣x≤﹣1,即lnx≤x﹣1,再分别令![]() ,
,![]() ,后利用不等式的性质两式相加,得到一个不等关系式,化简即可证出结论.
,后利用不等式的性质两式相加,得到一个不等关系式,化简即可证出结论.
解答:
解:(I)因为![]() ,
,
所以f′(x)=x﹣f′(2).(2分)
令x=2,得f′(2)=1,
所以f(x)=![]() .
.
(II)解:设F(x)=f(x)+g(x)=lnx﹣x,
则F′![]() ,(5分)
,(5分)
令F′(x)=0,解得x=1.(6分)
当x变化时,F(x)与F′(x)的变化情况如下表:
| x | (0,1) | 1 | (1,+∞) |
| f′(x) | + | 0 | ﹣ |
| f(x) | ↑ | 极小值 | ↓ |
所以当x=1时,F(x)max=F(1)=﹣1.(8分)
因为对于任意x∈(0,+∞),都有f(x)+g(x)≤a成立,
所以a≥﹣1.(9分)
(III)证明:由(II),得F(x)=lnx﹣x≤﹣1,即lnx≤x﹣1,
令![]() ,得
,得![]() ,
,
令![]() ,得
,得![]() ,(11分)
,(11分)
所以![]()
因为a1+a2=1,
所以![]() ,(13分)
,(13分)
所以a1lnx1﹣a1ln(a1x1+a2x2)+a2lnx2﹣a2ln(a1x1+a2x2)≤0,
即a1lnx1+a2lnx2≤(a1+a2)ln(a1x1+a2x2)=ln(a1x1+a2x2),
所以![]() ,
,
所以![]() (14分)
(14分)
点评:
本题考查了导数在最大值、最小值问题中的应用,及利用导数研究函数的单调性,考查了利用导数求函数在闭区间上的最值,考查了函数恒成立问题,是中档题.

 ,
, .
. ,
, 。
。 的单调区间;
的单调区间; ,曲线C与其在点
,曲线C与其在点 处的切线交于另一点
处的切线交于另一点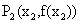 ,曲线C与其在点
,曲线C与其在点 ,线段
,线段
 (Ⅰ)(ii)的正确命题,并予以证明。
(Ⅰ)(ii)的正确命题,并予以证明。