题目内容
已知函数f(x)= sin2xsinφ+cos2xcosφ-
sin2xsinφ+cos2xcosφ- sin(
sin( +φ)(0<φ<π),其图象过点
+φ)(0<φ<π),其图象过点 .
.
(1)求φ的值;
(2)将函数y=f(x)的图象上各点的横坐标缩短到原来的 ,纵坐标不变,得到函数y=g(x)的图象,求函数g(x)在[0,
,纵坐标不变,得到函数y=g(x)的图象,求函数g(x)在[0, ]上的最大值和最小值.
]上的最大值和最小值.
解:(1)因为f(x)= sin2xsinφ+cos2xcosφ-
sin2xsinφ+cos2xcosφ- sin(
sin( +φ)(0<φ<π),所以f(x)=
+φ)(0<φ<π),所以f(x)= sin2xsinφ+
sin2xsinφ+ cosφ-
cosφ- cosφ=
cosφ= sin2xsinφ+
sin2xsinφ+ cos2xcosφ=
cos2xcosφ= cos(2x-φ).3分
cos(2x-φ).3分
因为该函数的图象过点( ,
, ),则
),则 =
= cos(
cos( -φ),即cos
-φ),即cos -φ)=1.因为0<φ<π,所以
-φ)=1.因为0<φ<π,所以



练习册系列答案
相关题目
 个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图象的函数解析式是( )
个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图象的函数解析式是( )
 ,则
,则 的最小值为( )
的最小值为( ) B、
B、  C、
C、  D、
D、
 的值为___________.
的值为___________. ,
, ,则
,则 是
是 成立的 ( )
成立的 ( ) ,则
,则 在
在 时的值域是 .;又若将函数
时的值域是 .;又若将函数 的图象向左平移
的图象向左平移 个单位长度得到的图象恰好关于直线
个单位长度得到的图象恰好关于直线 对称,则实数
对称,则实数 的最小值为 .
的最小值为 . 在点
在点 处的切线与直线
处的切线与直线 平行,则实数
平行,则实数 等于
等于 (C)-2 (D)2
(C)-2 (D)2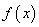 是定义在R上的周期为2的奇函数,当
是定义在R上的周期为2的奇函数,当 时,
时,
 B.
B. C.
C. D.
D.