题目内容
(08年安庆市二模)(14分)若函数![]() .
.
(1)求方程![]() 的实数根;
的实数根;
(2)若方程![]() (a为实数)在R上有三个不同的实数根,求实数a的取值范围.
(a为实数)在R上有三个不同的实数根,求实数a的取值范围.
解析:(1)![]()
![]() ………………………………………4分
………………………………………4分
(2)由![]() ,得
,得![]()
当![]() 或
或![]() 时,
时, ![]() 当
当![]() 时,
时, ![]() 所以在
所以在![]() 和
和![]() 上
上![]() 单调递增, 在
单调递增, 在![]() 上
上![]() 单调递减,在
单调递减,在![]() 上
上![]() 的极大值为
的极大值为![]() 在
在![]() 上
上![]() 的极小值为
的极小值为![]() ……………………………8分
……………………………8分
函数方程![]() 在
在![]() 上有三个不同的实数根,即直线
上有三个不同的实数根,即直线![]() 与函数
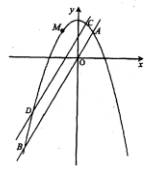
与函数![]() 的图象有三个交点. 由
的图象有三个交点. 由![]() 的大致图象可知, 当
的大致图象可知, 当![]() 时,
时,
直线![]() 与函数
与函数![]() 的图象没有交点;
的图象没有交点;
当![]() 时, 直线
时, 直线![]() 与函数
与函数![]() 的
的
图象有两个交点;当![]() 时,直线
时,直线![]() 与函数
与函数![]() 的图象有三个交点.
的图象有三个交点.
因此实数![]() 的取值范围是
的取值范围是![]() . ………………………………14分
. ………………………………14分


练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目